There are many ways to solve this problem. See the Hints for suggestions of other lines of investigation you might like to pursue to find other solutions.

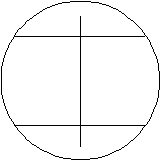
Andrei from Tudor Vianu National College, Bucharest, Romania has come up with an unexpected arrangement of the sticks. Here is Andrei's solution:

I chose to make $2$ segments of the unit, each of area a quarter of the unit circle, and the remained part of the circle to be divided into two equal parts, as shown in the figure. Let $x$ be the central angle determined by the segment. The area of the segment is: $${1\over 2}\left(x - \sin x\right).$$ And it must be a quarter the area of the circle so: $${1\over 2}\left(x - \sin x\right)= {\pi \over 4} .$$

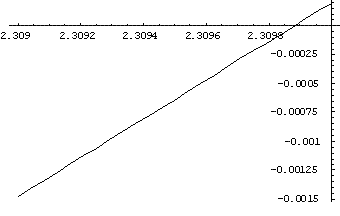To find a better approximation I used this graph. Plot $\left[x - \sin [x]- {\pi \over 2}, {x, 2.309, 2.31}\right]$ So $x \approx 2.3099$.

The length of the chord determined by the central angle $x$ in the circle of unit radius is : $$L = 2 \sin \left({x\over 2}\right) = 1.829$$ It is evident that $L$ is greater than the distance between the two parallel chords and is less than the diameter so that the problem has a solution.