Games Related to Nim

'Games Related to Nim' printed from https://nrich.maths.org/

Show menu

This small group of activities is taken from the Mathematical Games Archive on the NRICH site. They all have a related structure that can be used to develop the skills of strategic planning and reasoning as well as ideas of analogy.
Students at all levels of ability and age can access them. At the most basic level, they offer opportunities for practising arithmetical skills. At a higher level, they can be used to promote mathematical discussion by demanding detailed and reasoned explanations for a winning strategy, or an explanation of the mathematics that links the games.

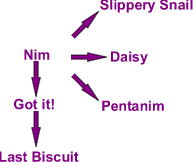
Suggested Progression

Links

Several of the games link into one another. One suggestion is given below. Can you see and describe the similarities between all of these games?

Links to the Framework

The following objectives are to be found in the Frameworks for teaching mathematics for Key Stages 1, 2 and 3, and apply to the activities in this theme.

Solve mathematical problems or puzzles, recognise simple patterns and relationships, generalise and predict.
Understand addition and subtraction mental calculation strategies.
Use letter symbols to represent unknown numbers or variables.
Represent problems mathematically.
Explain and justify methods and conclusions.
Use logical argument to establish the truth of a statement.
Solve increasingly demanding problems and evaluate solutions.
Present a concise, reasoned argument, using symbols, diagrams, graphs and related explanatory text.
Suggest extensions to problems, conjecture and generalise.

Daisy

Play the game.

Try to work out a winning strategy.

Does one of the players have the advantage?

NIM

Start playing this with 7 counters.

Try to work out a winning strategy.

Does it matter who goes first?

Now play with 9 counters.

Try to work out a winning strategy.

Is it preferable to go first or second?

Can you find a generalisation about the winner for any number of counters?

Got It!

Play the game on line.
Start with the Got It! total of 15, using the numbers 1, 2, 3, 4 or 5.
Try to work out a winning strategy.
Does it matter who goes first?
What is the connection between NIM and Got It!?
Now change the target number, but keep the numbers 1, 2, 3, 4 and 5.
Does this alter whether it is preferable to go first or second?
Can you write a mathematical statement to link the target number to the winning player?
Try to find a generalisation for who would win for any target number, and any group of consecutive numbers from 1 to b.
Try to find a generalisation for who would win for any target number, and any group of consecutive numbers from a to b.

Slippery Snail

Play the game and see if you can find a winning strategy.

Does it matter who goes first?

What happens if there are more or less spots to start with?

Does it matter if the stars are in different places?

Make up your own Slippery Snail game.

What is the connection between this and NIM?

Pentanim

Try to work out a winning strategy by playing the game.

Does it matter who goes first?

What is the connection with NIM?

Last Biscuit

An interesting and engaging version of the game .

Can you play and work out a strategy to ensure you always win using some of the strategies you have already learnt?

Can you explain any patterns you see?

Further activities linked with these on NRICH:

A whole list of NIM games:

One, Three, Five, Seven