Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Witch of Agnesi
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Sanjeet sent us this graph, showing the three curves on the same graph:
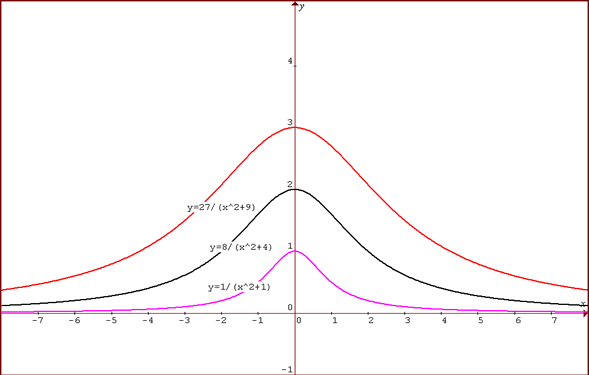
For different values of $a$ the graphs have the equation: $$y = {a^3\over (x^2+a^2)}$$ Differentiating $${dy\over dx} = - {2a^3x\over (x^2+a^2)^2}.$$ So the critical value is at $(0,a)$. Near this point, for small negative $x$ the gradient is positive and the function increasing and for small positive $x$ the gradient is negative and the function decreasing so this is a maximum point.
The value of $y$ is always positive so the entire graph lies above the $x$ axis and the graph is symmetrical about $x=0$ because $f(-x)=f(x)$.
For large $x$ the value of $y$ tends to zero so the line $y=0$ is an asymptote.
You may also like
Power Up
Show without recourse to any calculating aid that 7^{1/2} + 7^{1/3} + 7^{1/4} < 7 and 4^{1/2} + 4^{1/3} + 4^{1/4} > 4 . Sketch the graph of f(x) = x^{1/2} + x^{1/3} + x^{1/4} -x