Copyright © University of Cambridge. All rights reserved.
'Right Angles' printed from https://nrich.maths.org/
Show menu
Samantha and Shummus both realised that in order to create a triangle with a right angle, the band had to go through the centre of the circle. Shummus writes:
I noticed that the bands had to be started in the centre.Xianglong Ni notes that:
If we have 9 points on the circle then you can't create a right-angle using the points. This is so because a right angle is inscribed in a semicircle; It is facing a diameter. But you can only create a diameter when there is an even amount of points on the circle. If the number of points on the circle is even then yes. If the number is odd then no.
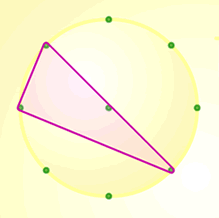
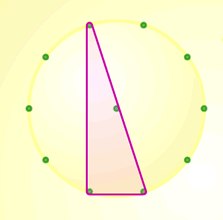
Rachel from Newstead sent us a few diagrams to illustrate examples of right-angled triangles in circles with an even number of points.
Indika of Helena Romanes 6th Form
College sent us her explanation for why the band must go through
the centre of the circle:
The only way that a right angle triangle
can be created between 3 points round the edge is when the angle
subtended at the centre by two of the points is 180 degrees, this
therefore proves that two of the points have to be opposite each
other (this means having an equal number of pegs).
This is because the angle subtended at the centre by two points are
exactly double the angle subtended at the edge by the same points.
This rule will apply to all circles, i.e. there will be a right
angled triangle if two pegs are placed opposite each other.
If you haven't met this idea before, you may want to look at another problem from August 2005, Subtended angles
Here are another couple of examples of right-angled triangles using the same eight-point and ten-point circles that Rachel used: