Copyright © University of Cambridge. All rights reserved.
'Flower' printed from https://nrich.maths.org/
Show menu
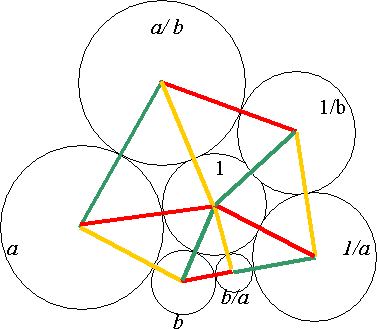
You are given a circle of radius 1 unit and two circles of radius $a$ and $b$ which touch each other and also touch the unit circle. Prove that you can always draw a 'flower' with six petals (as in the sketch) with the unit circle in the middle, and six circles around it having radii $a$, $b$, $b/a$, $1/a$, $1/b$ and $a/b$, such that each outer circle touches the unit circle and the two circles on either side of it.
[Note: this diagram is not drawn accurately. Drawing your own more accurate diagram may help you to do the question.]