The angle between two circles at the point of intersection is the angle between the tangents to the circles at that point contained in the overlapping area or lune. Prove that, for any two circles, the angles at both points of intersection are equal.

Three circles intersect at the point $D$ and, in pairs, at the points $A,\ B$ and $C$ so that the arcs $AB$, $BC$ and $CA$ form a curvilinear triangle with interior angles $\alpha$, $\beta$ and $\gamma$ respectively. The diagrams show two possible cases. Prove that, for any three such circles, $\alpha + \beta + \gamma = \pi$.

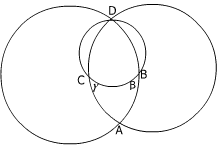
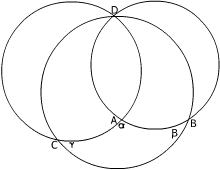
When you have done this question you might like to consider what happens on the surface of a sphere where instead of a flat surface (Euclidean geometry) you are working on a surface with positive curvature (Spherical or Elliptic geometry). See the article