Copyright © University of Cambridge. All rights reserved.
'Tricky Track' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This activity gives children the opportunity to grapple with experimental vs theoretical probability, in an accessible and appealing context. It will be essential for learners to discuss their ideas with others as they work on the problem. This problem assumes children understand that all numbers on the
standard dice are equally likely to be thrown.
Possible approach
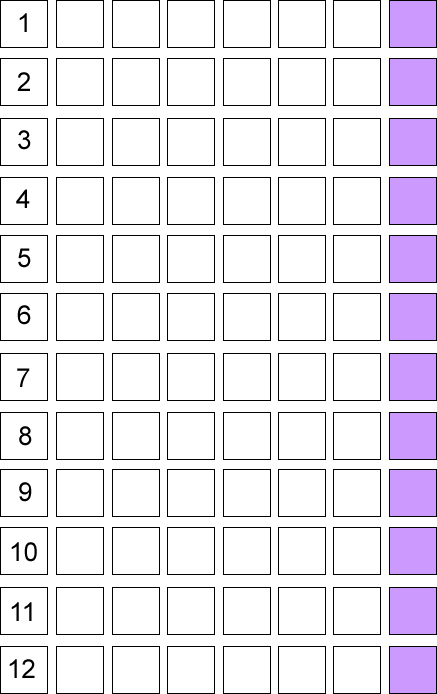
A good way to introduce this activity would be to use it as a game initially. Display the image of the board on an interactive whiteboard (you could do this from the image in the problem or from this sheet) and create twelve draggable counters, six in one colour
and six in another colour. Suggest to the class that they're going to play a game with one half against the other, and allocate a colour to each half. You can then invite learners to place their six counters on the numbers of their choice, or you could position them yourself and deliberately disadvantage one team (for example by placing their counters on the $1$, $2$, $3$, $10$, $11$, $12$). Once
the counters have been placed, explain that you will throw two dice (it can be helpful if these are different colours) and the counter on that total will move one place to the right. The winning team will be the team that gets the first counter to a purple square. Depending on the class' experience, you may find that there is some objection before the game begins! In this instance, you could
invite pupils to predict which team will win and give a reason for their prediction.
Having played the game as a whole group, you can then set the children off on the task of investigating which numbered counter reaches the purple box first. Each pair will need a copy of the board and twelve counters, or they could use squared paper. Will it always
work out in the same way as the game they played? If each pair works together, then you can collate results from the whole group to display on the board.
Encourage children to talk to each other about the results. Can they explain them? Draw out explanations that focus on the number of ways in which each total is possible. This can then lead into a full analysis of the number of ways of making each total. Challenge pairs to make a start on this themselves and encourage them to record the possibilities in whatever way suits them.
After a suitable period, bring the whole group together to discuss progress. At this point, learners could share the different ways they have of being systematic and you could take up one way to focus on. This might be, for example, making a list of all pairs of numbers thrown, starting with one die always being $1$: $1$ $1$, $1$ $2$, $1$ $3$, $1$ $4$ etc and then finding the totals.
Alternatively, some may start with the total and find all the ways to make it. Encourage the group to be critical - are they sure there aren't any repetitions? (This is where having differently coloured dice is helpful!) How do they know they have all the ways?
You may wish to leave the group to think about whether the most likely total will ALWAYS win in this activity. Why or why not? This is the crux of experimental versus theoretical probability and can be hard for children to understand. How could the activity be changed so that we can be more certain of the outcome? (There could be many more squares in each row, for example.)
Key questions
Which numbered counter do you think will get to the purple box first? Why?
How can you get a total of $1$ ... $2$ ... $3$ etc?
How will you make sure you have found all the possible totals?
Are you sure all your ways are different?
How will you record what you do?
Will the same numbered counter always reach the end first? Why?
Possible extension
Children could ask their own "what if ...?" questions, such as "What would happen if there were fewer boxes in each row?"; "What would happen if I used different dice?"; "What would happen if I found the difference between the two numbers rather than their total?" etc. You may find the interactive spinners in this
problem helpful.
Possible support
Everyone will be able to join in this activity to see which counter reaches the end first. If learners are experiencing difficulties with finding all possible combinations, you could ask them to write each combination on a separate small bit of paper, perhaps using coloured pencils, one colour for each of the dice. Then, pairs can arrange the combinations into a pattern which will help them
see any they have missed out.