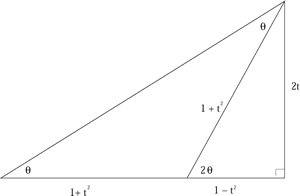
Use the diagram to prove the double angle formula, where $t=\tan \theta$: $$\tan2\theta = {2t\over {1-t^2}},\quad \sin2\theta = {2t\over {1+t^2}},\quad \cos2\theta = {{1-t^2}\over {1+t^2}}$$


The point $P'=(p',q')$ is the image of the point $P=(p,q)$ after reflection in the line $y=mx$. To find $(p',q')$ use the fact that the midpoint of $PP'$ is on the line $y=mx$ and the line segment $PP'$ is perpendicular to the line $y=mx$ and show that $$p'=p\cos2\theta + q\sin2\theta,\ q'=p\sin2\theta - q\cos2\theta\quad (1)$$ where $m=\tan\theta$. Hence establish another proof that the matrix

$$T_2= \left( \begin{array}{cc} \cos 2\theta &\sin2\theta \\ \sin2\theta &-\cos2\theta \end{array} \right) $$

gives a reflection in the line $y=x\tan\theta$. The point $P''=(p'',q'')$ is the image of the point $P'$ after reflection in the line $y=x\tan\phi$. Apply the transformation $$T_2' = \left(\begin{array}{cc} \cos 2\phi &\sin2\phi \\ \sin2\phi & -\cos2\phi\end{array}\right)$$ to the point $P'=(p',q')$ to find the coordinates of the point $P''$ in terms of $p, q, \theta$ and $\phi$. Hence show that the combination of two reflections in distinct intersecting lines is a rotation about the point of intersection by twice the angle between the two mirror lines. What is the effect of the two reflections if the lines coincide (i.e. $\theta=\phi$)?