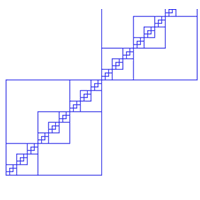
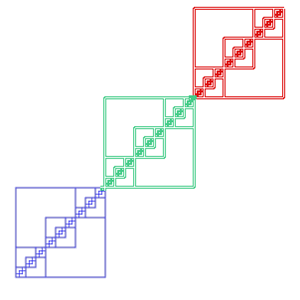
Below are two diagrams concerned with a sequence of squares

Both are based on the following procedure:

TO SQUARE :S :N
IF :S < 2 [ STOP]
REPEAT 2 [ REPEAT :N [ FD :S RT 90 FD :S LT 90] LT 180]
SQUARE :S/3 :N * 3
END

try SQUARE 120 3

Why not experiment with the procedure? Vary the value of S or N. Why not create a sequence of embedding hexagons? Pentagons? Pentagrams?

Alternatively:

Why not create your own fractals using recursion?

Explore further these well known procedures:

TO FIB :X :Y
PR :Y WAIT 60
FIB :Y :X + :Y
END

try FIB 1 1 or FIB 2 4 or FIB 3 5..............

or this:

TO SQ :X :A
PR :A
WAIT 60
SQ :X + 1 :A + 2 * :X - 1
END

try SQ 1 -2 or SQ -2 -2 or SQ 1 0....................

Devise your own procedures for generating sequences