Into the wilderness
Let's go further and see what happens when we multiply two complex numbers together!
Age
14 to 18
Challenge level
Problem
This resource is part of our Adventures with Complex Numbers collection
This activity follows on from Strolling Along.
To multiply two complex numbers we can expand brackets, taking care to remember that $i^2 = -1$.
For example:
$$\eqalign{\left(4+2i\right)\left(\frac{7}{5}- 3i\right) &= \frac{28}{5} + \frac{14}{5}i - 12i - 6i^2 \\ &=
\left(\frac{28}{5} + 6\right) + \left(\frac{14}{5} - 12\right)i \\ &= \frac{58}{5} - \frac{46}{5}i.}$$
But what's happening geometrically when we multiply complex numbers?
We have created the GeoGebra interactivity below for you to explore.
$z_3$ is the product $z_1z_2$.
You can move the complex number $z_1$ around the circle, and you can move $z_2$ anywhere on the grid. Use the slider $a$ to change the radius of the circle.
Choose a radius, and a position for $z_2$.
Move $z_1$ around the circle.
What do you notice?
Now explore what happens when you fix $z_1$ and move $z_2$.
You may find it helpful to "Show Lines" joining each point to the origin.
For which values of $z_2$ does the line through $z_1$ and $z_3$ pass through the origin?
What is special about the positions of $z_1$ for which $z_2$ and $z_3$ are equidistant from the origin?
Now that you have explored multiplication of numbers, you might like to try the Complex Puzzle.
Student Solutions
Thank you very much to Navjot from Sherborne Qatar, Vicente from King's College Alicante in Spain and Samantha from Tanglin Trust School in Sigapore, for the solutions that they submitted. The solution below draws on their observations and explanations.
Thank you also to Amrit from Hymers College in the UK, who sent in more detailed proofs. You can see these via the link at the bottom of the solution.
Keeping $z_2$ and $a$ fixed and moving $z_1$ around the circle, $z_3$ also moves in a circle centred at the origin. The angle between $z_1$ and $z_3$ doesn't appear to change:
Image
Image
Image
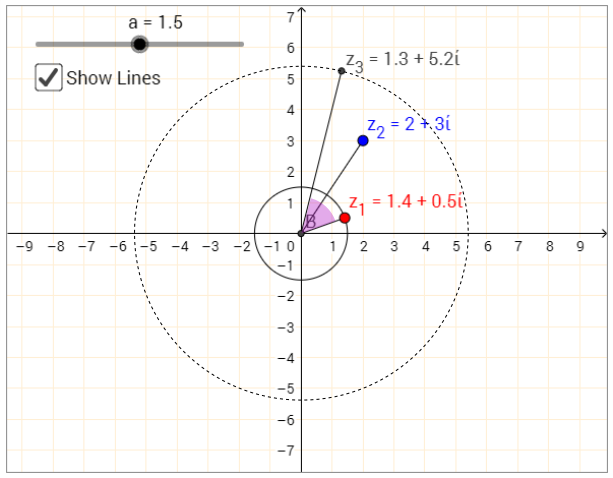
Keeping $z_1$ fixed and moving $z_2$ around, now the angle between $z_2$ and $z_3$ appears to stay the same:
Image
Image
Image
Putting $z_2$ on the real axis makes the line through $z_1$ and $z_3$ pass through the origin. This helps to see that the green angle between $z_2$ and $z_3$ is the same as the angle between $z_1$ and the real axis!
Image
So the angle between $z_2$ and $z_3$ is the same as the angle between $z_1$ and the real axis.
Similarly, the angle between $z_1$ and $z_3$ is the same as the angle between $z_2$ and the real axis, as shown below. This explains why, when $z_2$ is real, so makes an angle of $0^\circ$ with the real axis, $z_1$ and $z_3$ lie on the same line through the origin - so the angle between $z_1$ and $z_3$'s line segments is $0^\circ$.
Image
How this relates to what we saw in Strolling Along
In Strolling Along, we saw that multiplying by a positive multiple of $i$ resulted in an anticlockwise rotation through $90^\circ$, while multiplying by a negative multiple of $i$ resulted in a clockwise rotation through $90^\circ$.
Well, the angle between the real axis and the imaginary axis is $90^\circ$, so this agrees with what we have just seen. The direction of a rotation from the positive real axis is anticlockwise to reach a positive multiple of $i$, but clockwise for negative multiples of $i$. This is shown on the diagrams below, which show the same multiplications that appear in the solution to Strolling Along:
Image
When $z_2=0.5i$, the angle from the positive real axis to $z_2$ is $90^\circ$ anticlockwise, and the angle from $z_1$ to $z_3$ is also $90^\circ$ anticlockwise.
Image
When $z_2=-3i$, the angle from the positive real axis to $z_2$ is $90^\circ$ clockwise, and the angle from $z_1$ to $z_3$ is also $90^\circ$ clockwise.
Making $z_2$ and $z_3$ equidistant from the origin
Recall that moving $z_1$ around with $a$ and $z_2$ fixed, $z_3$ was always the same distance from the origin. So to make $z_3$ closer to or further from the origin, we should change $a$.
Compare the diagrams below to see that making $a$ larger makes $z_3$ further from the origin, and making $a$ smaller makes $z_3$ closer to the origin:
Image
Image
Image
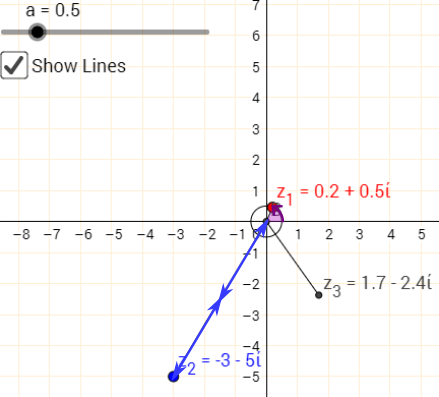
When $a$ was $2$ or $3$, $z_3$ was further from the origin than $z_2$ was. When $a$ was $0.5$, $z_3$ was closer to the origin than $z_2$ was. When $a=1$, $z_2$ and $z_3$ are equidistant from the origin. To make this easier to see, the circle centred at the origin going through $z_2$ is shown on the diagram below:
Image
It looks like $a$ is the scale factor between the lengths of the line segments joining $z_2$ and $z_3$ to the origin.
We can check this by using Pythagoras' Theorem to find the distances from the origin $z_2$ and $z_3$.
$z_2=1-3i$, so the distance from the origin to $z_2$ is $\sqrt{1^2+3^2}=\sqrt{10}=3.16$ to 2 decimal places.
When $a=2$, we would expect the distance from the origin to $z_3$ to be $2\times3.16=6.32$. In this case, $z_3=5-3.9i$, with each coefficient given to 1 decimal place. So the distance from the origin to $z_3$ is approximately $\sqrt{5^2+3.9^2}=\sqrt{40.21}=6.3$ to 1 decimal place.
When $a=3$, we would expect the distance from the origin to $z_3$ to be $3\times3.16=9.48$. In this case, $z_3=7.5-5.8i$, with each coefficient given to 1 decimal place. So the distance from the origin to $z_3$ is approximately $\sqrt{7.5^2+5.8^2}=\sqrt{89.89}=9.5$ to 1 decimal place.
When $a=0.5$, we would expect the distance from the origin to $z_3$ to be $0.5\times3.16=1.58$. In this case, $z_3=1.2-i$, with each coefficient given to 1 decimal place. So the distance from the origin to $z_3$ is approximately $\sqrt{1.2^2+1^2}=\sqrt{2.44}=1.6$ to 1 decimal place.
So when we multiply $z_2$ by a complex number $z_1$ on a circle with radius $a$, the product $z_3$ can be described as a transformation of $z_2$. It is an enlargement, centred at the origin, with scale factor $a$, and a rotation, also centred at the origin, through the angle from the positive real axis to $z_1$.
Some examples are illustrated below. On the left, the angle from the positive real axis to $z_1$ is shown in purple and the distance from the origin to $z_2$ is shown in blue. On the right, the purple angle is placed between $z_2$ and $z_3$ to see the rotation, and blue arrow(s) are placed along the line segment from the origin to $z_3$ to show its length.
Image
Image
Image
Image
Why does this happen?
Image
$a$ is the distance from the origin to $z_1$, which we can find using Pythagoras' Theorem as $\sqrt{c^2+d^2}$.
Recall from Strolling Along that multiplying by the real number $c$ is the same as an enlargement centred at the origin with scale factor $c$. Recall also that multiplying by $di$ represents a rotation of $90^\circ$ anticlockwise about $0+0i$ and an enlargement centred at the origin with scale factor $d$. This is easier to visualise when $c$ and $d$ are positive, as shown on the right. The same diagrams with negative $c$ and $d$ are all shown at the bottom of this explanation.
$z_3=z_1z_2=(c+di)z_2=cz_2+diz_2$. This is shown in this way on the diagram below - as the sum of two vectors.
Image
Now consider the two yellow triangles in the diagram below. They are similar, since both of them have a pair of perpendicular sides with lengths in the ratio $c:d$. So the angle between $z_2$ and $z_3$ is the same as the angle between $z_1$ and the real axis. The scale factor of the enlargement from the small triangle to the large triangle is the same as the distance from the origin to $z_2$. So the distance from the origin to $z_3$ is equal to $a=\sqrt{c^2+d^2}$ multiplied by the distance from the origin to $z_2$.
Image
The diagrams below show the same process but for a $z_1$ with $c$ and $d$ negative.
Image
$c$ and $d$ are negative (but $a=\sqrt{a^2+b^2}$ is still positive)
Image
Multiplication by a negative real number moves $z_2$ to the other side of the origin. We can also now understand this as rotation by the $180^\circ$ angle from the positive real axis to the negative real axis!
Multiplication by a negative multiple of $i$ is a rotation $90^\circ$ clockwise and an enlargement with a positive scale factor.
Image
The angle between $cz_2$ and $z_3$ is the same as the angle between the negative real axis and $z_1$. The sum is $180^\circ$ when this angle is added to the angle from the positive real axis to $z_1$, or to the angle from $z_2$ to $z_3$. So the angle from $z_2$ to $z_3$ is the same as the angle from the positive real axis to $z_1$.
So the product of two complex numbers $z_1$ and $z_2$ can be found on an Argand diagram by applying to a rotation and an enlargement, both centred at the origin, to one of the complex numbers.
$z_2$ could be enlarged by a scale factor $a$, where $a$ is the distance from the origin to $z_1$, and rotated by the angle from the positive real axis to $z_1$.
Equivalently, $z_1$ could be enlarged by a scale factor $b$, where $b$ is the distance from the origin to $z_2$, and rotated by the angle from the positive real axis to $z_2$.
This is also frequently described as:
- The distance from the origin to $z_3$ is the product of the distance from the origin to $z_1$ and the distance from the origin to $z_2$
- The angle from the positive real axis to $z_3$ is the sum of the angles from the positive real axis to $z_1$ and to $z_2$
Click here to see Amrit's proofs.