A single knight's move takes it two squares parallel to one side of the board and one square parallel to the other side.Any such move always takes the knight to a square of the opposite colour (you might like to check this). So, as all the squares on the diagonal are the same colour, the number of moves to go to a square along the diagonal from the starting point must be even because it must take an even number of moves to get from a square of one colour to a square ofthe same colour. We first find the smallest number of moves needed to go from one corner to the opposite corner of a $99$ by $99$ square board and then solve the problem for boards of any size.

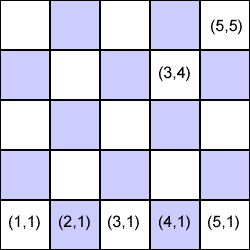Label the squares: the bottom left-hand corner square as $(1,1)$, other squares across the bottom row as $(2,1)$, $(3,1)$ etc. and, in general, the square in the $x$ column across and the $y$ row up as $(x,y)$. Notice that we are labelling whole squares here and we can think of a lattice of whole number co-ordinates with points at the centres of the squares.

In this article we shall call a move from one square on the diagonal of a chess board to the next a 'diagonal step'.

A knight can do two types of moves...

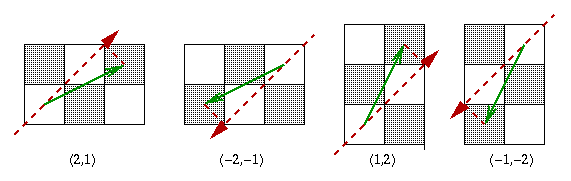
We should make a comment about notation here because you may meet vectors written in columns in school work, for example $\left( \begin{array}{c} 2 \\ 1 \end{array} \right)$ rather than $(2,1)$, which is just another way of writing the same thing.

The other type of move has the effect of taking the knight only half a diagonal step forward or backwards in the direction of the diagonal and we denote these moves by the vectors $(2,-1)$, $(-2, 1)$, $(1,-2)$, and $(-1,2)$ as shown in the diagram below.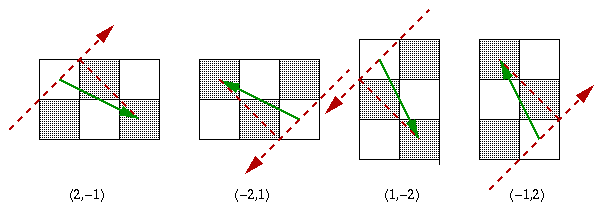

Putting moves together...

We add vectors by adding the components separately, for example:

$$(2,1) + (-2,1) = (0,2)$$

$$(2,1) + (2,1) + (2,1) + (1,2) = (7,5)$$

We can take multiples of vectors (to denote a move repeated several times) by multiplying each component separately, for example repeating the move $(2,1)$ three times is given by $3$ times $(2,1)$, which we write as $3(2,1)$ or $(6,3)$. We see that

$$(2,1) + (2,1) + (2,1) + (1,2) = 3(2,1) + (1,2) = (6,3) + (1,2) = (7,5)$$

From a starting square labelled $(x,y)$ these four moves take the knight to the square

$$(x,y) + 3(2,1) + (1,2) = (x+7,y+5)$$

You can check all this vector algebra practically by counting squares on a board.

A knight can move from square $(1,1)$ to square $(99,99)$ in $66$ moves by doing the move $(1,2)$ $34$ times, the move $(2,-1)$ once, and the move $(2,1)$ $31$ times. It will finish at the square given by

$$(1,1) + 34(1,2) + (2,-1) + 31(2,1) = (99,99)$$

Smallest number of moves...

As the knight can't move more than $\frac{3}{2}$ diagonal steps along the diagonal in any one move, it can't move more than $\frac{3m}{2}$ diagonal steps in $m$ moves. From this we get $\frac{3m}{2} \geq 98$ which means that $m \geq \frac{196}{3}$.

Of course $m$ is a whole number so this tells us that $m = 66$ gives the fewest possible moves and we have shown how this can be done.

Check that the moves described for the $99$ by $99$ board will not take the knight off the edge of the board at any stage and in general this is not a problem because the moves can be taken in any order.

Let us now consider the problem for an $n$ by $n$ square board. As before the knight has to move $(n-1)$ diagonal steps in the direction of the diagonal and it can't move more than $\frac{3}{2}$ diagonal steps in this direction in any one move so it can't move more than $\frac{3m}{2}$ diagonal steps in $m$ moves. From this we get the inequality $\frac{3m}{2}\geq (n -1)$.

The knight has to make slightly different combinations of moves according to whether or not $n$ is divisible by $3$ so we consider all the possibilities.

Case 1: $n = 3k + 1$

The knight makes the move $(1,2)$ exactly $k$ times then the move $(2,1)$ exactly $k$ times. This is a total of $2k$ separate moves and it takes the knight to the end position given by:

$$(1,1) +k (1,2) +k (2,1) = (1,1) + (k, 2k) + (2k,k) = (3k+1,3k+1)=(n,n)$$

The reader can check this for $n = 4, n=7$ etc. To show that it can't be done in fewer moves we use the inequality $\frac{3m}{2}\geq(n-1)$ and substitute $n = 3k + 1$ to get:

$3m \geq 2(n - 1) = 6k$

and, dividing this by $3$, we get $m\geq 2k$ and so $m = 2k$ is the smallest number of moves.

Case 2: $n = 3k + 2$

The knight makes the move $(1,2)$ exactly $k$ times, then the move $(2,-1)$ once followed by the move $(-1,2)$ once, and finally the move $(2,1)$ exactly $k$ times. This is a total of $2k+2$ separate moves and it takes the knight to the end position given by:

\begin{eqnarray}(1,1) +k(1,2) + (2,-1) + (-1,2) +k(2,1)&=& (1,1) + (k, 2k) + (2,-1) + (-1,2) + (2k,k)\\ &=& (3k+2, 3k+2) \\&=& (n,n) \end{eqnarray}

The reader can check this for $n = 5, n=8$ etc. To show that it can't be done in fewer moves we use the inequality $\frac{3m}{2}\geq(n-1)$ and substitute $n = 3k + 2$ to get:

$3m \geq 2(n - 1) = 6k + 2 $

and, dividing this by $3$, we get $m \geq 2k + \frac{2}{3}$. We know that m is a whole number so it has to be at least $2k +1$ but, in addition to this, we know that m is an even number because the starting and finishing squares are the same colour, so m is at least $2k +2$.

Case 3: $n = 3k$

When $k=1$...

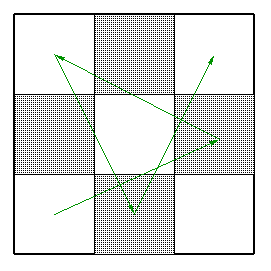It takes four knight's moves to cross to the opposite corner of a $3$ by $3$ board and this can be done as shown in the diagram below

When $k$ is greater than $1$...

The knight makes

• the move $(1,2)$ altogether $k+1$ times, adding up to the vector $((k+1),(2k+2))$,
• then the move $(2,-1)$ once,
• finally the move $(2,1)$ exactly $k-2$ times, adding up to the vector $((2k-4),(k-2))$.

To show that it can't be done in fewer moves we use the inequality $\frac{3m}{2} \geq (n-1)$ and substitute $n = 3k$ to get:

$$3m \geq 2(n- 1) = 2(3k - 1) = 6k -2$$

and, dividing this by $3$, we get

$$m \geq 2k - \frac{2}{3} $$.

As $m$ is a whole number this means that $m \geq 2k$ and so $ m = 2k$ is the smallest number of moves.