Skeleton Shapes

'Skeleton Shapes' printed from https://nrich.maths.org/

Show menu

Skeleton Shapes

Skeleton shapes are made with balls of modelling clay and straws.

This shows a cube and a skeleton cube:

How many balls of modelling clay and how many straws does it take to make the cube?

Here are some piles of modelling clay balls and straws:

piles of balls and straws: 6 straws with 4 balls, 9 straws with 6 balls, 8 straws with 5 balls, 12 straws with 8 balls, 18 straws with 12 balls

Look at the shapes below and decide which piles are needed to make a skeleton of each shape.

solid triangular prism, tetrahedron, cuboid, square pyramid and hexagonal prism

How do you know which piles go with which shape?

Why do this problem?

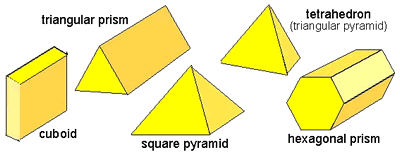
This problem helps children begin to become familiar with the various properties of common geometric solid shapes, concentrating on edges and vertices. It also helps in promoting discussion and experimentation. Naming the shapes should be a help during discussion and description of what has been done, rather than being an exercise in its own right.

Possible approach

Before doing this problem children should have had plenty of free play building with sets of solid shapes so that they begin to get a feel for their properties. They should also have chance to experiment with building skeleton shapes either with a specific kit or with drinking straws and modelling clay/plasticine.

You could start on the problem by asking the group to tell you what they know about cubes. Using a large cube, ask them to count the faces, the edges and the vertices (corners). (Avoid the word "side" which can be confusing when discussing 3D shapes and use instead "face" and "edge".)

After this you could encourage the group to work in pairs on the problem from a printed sheet so that they are able to talk through their ideas with a partner. It is essential that children have real 3D shapes to handle and count as they work and if at all possible they should have opportunity to experiment by making skeleton shapes as well. This sheet might be useful for recording for those children who would find making their own table for results difficult.

Key questions

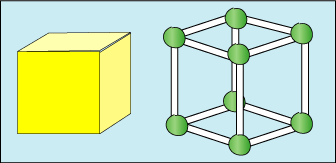
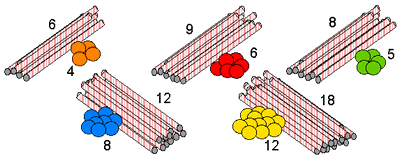
How many edges did you count? What does this tell you about the number of straws we need?
How many corners did you count? What does this tell you about the number of balls of modelling clay we need?
How many edges meet at this corner?

Possible extension

Children could find other solid shapes and continue the activity. They could also record by drawing the shapes they have used on isometric paper although this is rather tricky!

Possible support

Start by counting the faces on a cube - a large dice might be useful - and then the edges and finally the vertices. A non-permanent pen could be used to mark a real shape if children are having difficulty keeping track of their counting.