Copyright © University of Cambridge. All rights reserved.

'Coloured Edges' printed from http://nrich.maths.org/

Show menu


There is a set of tiles which are all different and coloured just on the edges. Each edge on a tile is a different colour. For example:
three squares, each square has edges of four different colours
Altogether $10$ different colours are used for the edges, and there is an equal number of edges of each colour used throughout the set.
The whole set of tiles is used to make a square. This has a green and blue border. There are no green or blue tiles anywhere in the square except on this border.
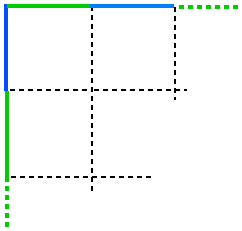part of arrangement of tiles in a square showing edges of tiles alternately green/blue round outside edge of large square
How many tiles are there in the set?