Square Corners

'Square Corners' printed from https://nrich.maths.org/

Show menu

Square Corners

Have a look at the three grids below.

What do you see?
What do you notice?

Once you have had chance to think, talk to someone else about your noticings.

Click below to read what some children noticed.

Miles said:

There are lots of spots. And I can see some of the spots are blue. The blue spots are joined to make shapes.

Freya said:

All the shapes have four sides. Some of the shapes are turned round.

Omar said:

I can see three red squares! They're different sizes.

Do you agree with Miles, Freya and Omar? Why or why not?

Now it is your turn...

Use the interactivity below to put blue counters on the grid.
Your challenge is to put as many counters on the grid as you can but none of them must lie at the corners of a square.

How many counters can you use without making a square?
How do you know that you cannot have more counters?

If you would prefer to work away from the computer, you might like to use a printable sheet (square grid or array of circles) with counters.

We would love to hear how you are going about this task!

This problem is taken from 'Mathematical Challenges for Able Pupils Key Stages 1 and 2', published by DfES.

Why do this problem?

This problem challenges pupils' understanding of the properties of squares in the sense that squares do not necessarily have to be orientated so that their sides are horizontal and vertical. It is also a good context in which to encourage children to find a systematic approach.

Possible approach

You could begin by playing the game Seeing Squares a few times as a class. This will provoke discussion amongst pupils about what makes a square a square, and you may wish to address the misconception that tilted squares are called 'diamonds'.

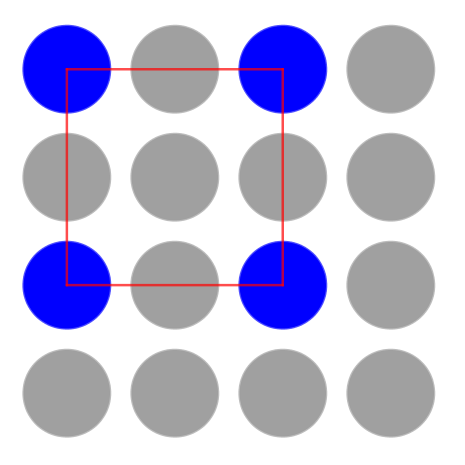
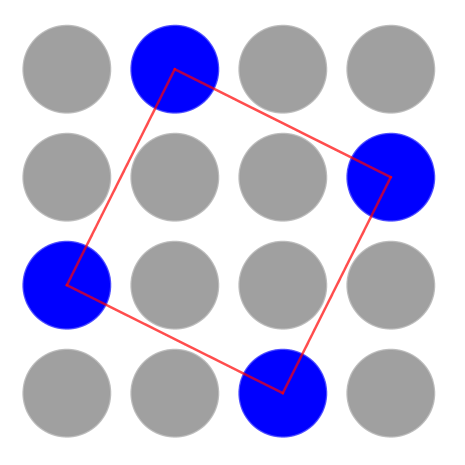
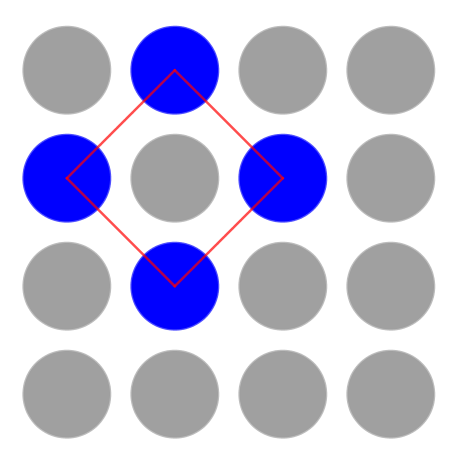
Introduce the problem by showing the three images and inviting the class to consider what they see. After talking with a partner, suggest that learners share their noticings. Try to encourage other members of the group to comment on, and question, the observations rather than you validating the contributions. Reveal the three children's comments in the problem and facilitate a discussion so that the class decides whether they agree or disagree with each one.

Using the interactive grid on the interactive whiteboard, help learners to understand the main challenge and ask them to begin to work on it in pairs. If they do not have access to the interactivity on tablets or computers, learners could use a large grid, of squares or an array of circles, with counters and/or this sheet of smaller grids. Remind them to check for squares!

After a suitable length of time, share results so far amongst the whole group. What is the largest number of counters so far? Ask a pair of learners to come up and recreate their arrangement of counters on the screen so that everyone can check there are no squares.

At this point, challenge the class to come up with a way of working that will ensure the largest number of counters is definitely found. How will they know that all arrangements have been tested? Some children may suggest a system based on, for example, placing counters on the grid from top left to bottom right and each time checking that a square has not been made. You could model the beginnings of a strategy and then give the class more time to investigate the problem. It may be that you split the group up to investigate different 'families' of arrangements.

In the plenary, you could discuss the solutions and what makes one arrangement of counters different to another. Will rotations and reflections be considered different or the same?

Key questions

How will you know that you have definitely found the largest number of counters?
Are you sure there aren't any squares on your grid?

Possible support

Pupils could start with a three by three grid.

Possible extension

Children could investigate larger grids and see whether there is a pattern to the number of counters by looking at smaller grids too. Is it possible to predict the largest number of counters in any size grid?

You might like to use the interactivity below to check solutions to larger grid sizes.