How can I support the development of early number sense and place value?
Introduction
By the time children leave primary school, we would like them to have a well-developed sense of number and a deep understanding of place value. In her articles Early Number Sense and Place Value: The Ten-ness of Ten, Jenni Back discusses what we mean by these two areas of mathematics, outlines relevant research findings and introduces some manipulatives which support their development. In this article, we expand on the key ideas and suggest mathematical activities which will help to develop these important aspects of mathematics.
Jenni suggests in the aforementioned articles that the first step towards a deep understanding of number and place value is having a strong sense of the numbers up to ten. From there, developing children's 'sense of ten' is essential as part of their understanding of place value and this also paves the way for mental calculation. In addition to this 'sense of ten', place value encompasses three other important ideas:
- Ordering - comparing numbers with each other
- Position - understanding how the place of a digit affects its value in any particular number
- Amount - knowing what the digits represent.
Below we take these five fundamental ideas (early number sense, sense of ten, ordering, position and amount) in turn and offer mathematical tasks to help develop each.
1. Early Number Sense
Dot Cards
In her Early Number Sense article, Jenni introduces us to 'dot cards' which are cards with dot stickers stuck on one side. Different arrangements of dots for a particular number help children see the structure of that number so that eventually it can be recognised using mental strategies, rather than by counting.
Jenni Way described a number of games using dot cards in her original number sense article. They are still as useful and motivating as they were when she wrote the article in 2001 and so we have gathered the games here for ease. The games help to develop children's number sense by offering different representations of numbers and by creating a motivating context in which to begin to add and subtract.
Hungarian Number Pictures
One of the ways in which we can help children develop their sense of number is by offering a range of different representations of numbers (see the Early Number Sense article). In From Objects and Images to Mathematical Ideas, Jenni decribes her observations of a class of 6-7 year olds in Hungary where the focus was the number six. A whole range of representations of six were shared with learners in a single lesson, for example the pattern of six on a die, the finger pattern of six, collections of six objects, collections of actions, Cuisenaire rods to make six, dominoes with six spots, Roman numerals to represent six, the symbol '6', six on a number line, six o'clock on an analogue clock face and coins worth six.
Also included in that lesson, and of particular note in this context, are 'number pictures' which are used by teachers in Hungary as a way of supporting children's understanding of numbers and their learning of number bonds to twenty. A template is used along with counters that are blue on one side and red on the other. Here is a picture of the template:
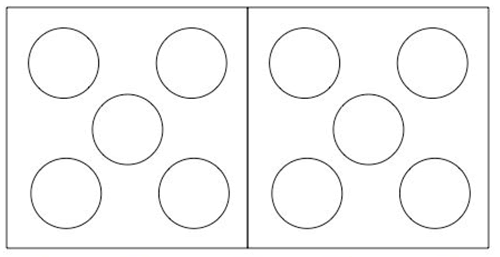
These 'number pictures' are based on the notion that we can instantly recognise numbers to five without counting (a skill called subitising - see Early Number Sense) and so arranging the number of dots in the holes on the template help. Different numbers can be shown in different colour dots for addition (this is where the double-sided counters are useful). Here is a downloadable sheet of the template along with coloured counters. Two sets will enable you to work with the numbers to twenty. The iconic representation will help learners to remember and visualise the number bonds.
NRICH tasks
If you are working with young children, take a look at our Early Years resources. Many of them offer contexts in which children might explore number. In particular, we would recommend Golden Beans, Dice, Playing Incey Wincey Spider and Number Rhymes, all of which will help develop children's sense of number from an early age.
Number Match is a group task, ideal for lower primary learners. It will help pupils grasp the 'threeness of three', for example, and offers different representations of numbers for children to interpret.
2. The Ten-ness of Ten
As Jenni indicates in her article Place Value: The Ten-ness of Ten, once children have developed a sense of the numbers up to ten, the next step is for them to have a strong 'sense of ten'.
Ten-frames
In that same article, Jenni introduces us to ten-frames, which are are two-by-five rectangular frames into which counters are placed to illustrate numbers less than or equal to ten. Jenni explains how ten-frames can 'prompt different mental images of numbers and different mental strategies for manipulating these numbers, all in association with the numbers' relationships to ten'.
Here we offer three games, all of which make use of ten-frames to help to develop children's understanding of ten as one of the most significant numbers in our number system.
3. Ordering
There are several tasks on the NRICH site which help children get to grips with this aspect of place value. In Next Domino, learners are required to extend sequences of dominoes. This will involve comparing the dominoes already in the sequence and identifying what is the same and what is different about them, before deciding on the missing dominoes. (And of course in order to do all that, some children will be subitising.)
That Number Square involves similar skills, but now in the context of higher numbers, as children are challenged to rebuild the hundred square from scratch. Coded Hundred Square takes the challenge up a level by including numbers 0 to 99 written in code. In order to reassemble the coded hundred square jigsaw, children will be comparing and ordering, but in addition they will draw on knowledge of the position of digits, leading us on to ...
4. Position
One of the fundamental ideas associated with place value is that the position of a digit in a number affects its value. So, for example in the number 126, the 6 is worth six ones, whereas in the number 164, the 6 is worth six tens. 6 Beads, Two-digit Targets, Five Steps to 50 and Largest Even are all NRICH lower primary tasks which will help learners come to a deep understanding of this aspect of place value. In fact, to some extent, these activities also involve some ordering and comparing but digit position is central.
For some higher level challenges which also focus on digit position, take a look at Which Scripts? and Some Games That May Be Nice or Nasty.
5. Amount
This final key element associated with place value refers to knowing that, for example, '6 tens' is equivalent to 'sixty'. Matching Numbers is a very accessible 'matching pairs' interactive game which focuses on interpreting numbers represented in different ways. Count The Crayons, another lower primary activity, also supports this aspect and leads on to encouraging children to work with groups of ten, termed 'unitising' (see Jenni's third article Place Value as a Building Block for Developing Fluency in the Calculating Process). How Would We Count? and Fingers and Hands offer similar challenges.
Of course, you will have noticed that the majority of NRICH tasks do not address just one single aspect of place value in isolation, rather they give contexts in which to make connections between several aspects at once.
The Gattegno Tens Chart
Similarly, the Gattegno tens chart is an invaluable resource in this context which can help to develop all aspects of place value. In his article, Journeys on the Gattegno Tens Chart, Alf Coles describes a project in which a Year 3/4 class (7-9 year olds) gained an awareness of place value and of the inverse relationship between multiplication and division. In his follow-up article, Alf outlines six classroom activities which progress from reading, writing and ordering numbers up to finding percentages of any number, all using the Gattegno chart.
Number Sense and Place Value in the New National Curriculum
Those of us teaching in England are currently (February 2013) in the transition phase between old and new national curricular. The new mathematics national curriculum contains more challenging content compared with the old version. In this context, therefore, we need to make sure we give children sufficient time to embed a sense of number and gain a deep understanding of place value. You may also be interested in Jenni's article Place Value as a Building Block for Developing Fluency in the Calculation Process. It discusses two further aspects of place value, exchange and unitising, which will help children to partition numbers and to calculate.
The new curriculum also presents an opportunity to introduce a bit of history. Children often struggle to see any reason why we should want to develop a place value system and would prefer to continue to adopt different symbols for successive digits. This is the time you could explore some historic systems such as Roman numerals and consider the problems they create with representation and calculation. 83 + 49 becomes LXXXIII + XLIX and the calculation depends on subtle interpretations of the 'I' and 'X' to take account of the fact that they mean one less than ten and ten less than fifty in the number XLIX. Calculations become very tricky with Roman numerals but it took human civilisations a long time to develop base ten number systems that overcame the difficulties. The Babylonians used a base 60 system and we can still see vestiges of this in our measuring systems for time and also for angles which involve multiples of 60.
In Conclusion
All the articles and activities we refer to above can be found in our Number Sense and Place Value Feature. We hope you enjoy working on these important mathematical ideas with your children and that their understanding is enhanced as a result.
Here is a PDF version of this article.