Copyright © University of Cambridge. All rights reserved.
'Mystery Matrix' printed from https://nrich.maths.org/
Show menu
We had a good number of solutions come in for this challenge. Firstly, we had a few solutions from children at Peak School in Hong Kong:
Victoria K & F
Our answers to your questions:
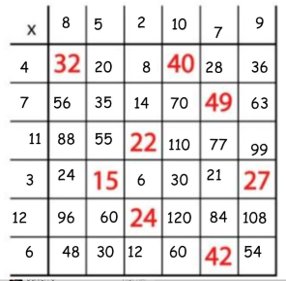
1) Yes, we can see how the grid has been constructed: horizontal x vertical black numbers = red number or another way to explain is: black number x black number = red numbers e.g: 2 that is horizontal x 6 vertical= 12 in red
2) The red numbers are the answers to the black numbers e.g 2x2= 4, 2x3 = 6, 2x4=8, 2x5=10 and so on
3) The red 6 is in that square because 2x3=6
4) There is a 45 in the right-hand corner because 9x5=45
Holly
The way the first square is constructed is the multiplication sign is in the corner and there are the numbers you have to multiply around the outside. The red numbers in the middle of the square are the answers the the multiplication question. You know the multiplication question by looking at the black number in the same row as the answer and the black number in the same
column as the red answer. The 6 is in that particular square because the black number above it is 3 and that black number to the right of it is 2. 3 x 2 = 6. Same for 45. Above it is 5 and to the right is 9. 9 x 5 = 45. I think the number that had to be doubled was 7. The grey numbers outside of the red lines are the “black numbers” and the
numbers inside of the red lines are the “red numbers”.
The way I started off was seeing which number around the outside would be obvious. I saw the 49 and I knew that it would be 7 x 7.
From doing that, I figured out the doubled number and what the black number to the right of 42 would be: a 6.
Then I looked at the column with 22 and 24 and I noticed that they were both multiples of 2. This meant that the 2 would be black number in the same column as 22 and 24. The black number in the same row as 22 would be 11, and the black number in the same row as 24 would be 12.
This crosses off 7, 7, 6, 12, 11, and 2. I started looking at what 15 and 27 had in common. They are both multiples of 3! The black number in that row is 3. The black number directly above 15 would be 5 as 5 x 3 = 15. The black number in the same column as 27 would be 9 because 9 x 3 = 27.
This leaves the numbers 4, 8, and 10 around the outside. I figured that 32 and 40 were multiples of 8 and 4, but then I remembered that 40 is a multiple of 10. This means 10 goes directly above the 40, 4 would be the black number in the same row as 40, and 8 would be directly above 32.
Then I
filled out all of the rest of the times tables. This is how I figure out the solution to mystery matix.
Thanks for reading!
Students from 5T at Ivanhoe School in Melbourne, Australia, sent the following picture of their completed grid, which agrees with Holly's fantastic reasoning above:
Pupils from Sefton Park Junior School in Bristol sent in the following:
To solve this problem, we first looked at the example grid and noticed that the numbers in red were answers to times table questions. The questions were written in black. Once we understood how the times table grid worked, we started trying to find the missing numbers.
First we looked at the multiples and tried to see which numbers we could multiply together (factors) to make that answer. We knew that 15 and 27 are both in the 3x table so that 3 could be filled out. We know 3x5 is 15 and 3x9 is 27.
Then we noticed that 22 and 24 are both multiples of 2 so we filled out that 2x11=22 and 2x12=24
One mistake we made was using the number 2 twice. We thought 2 would be in the answers for the 22 and 24 column and that it would be 2x16 = 32 but then we realised we could only use numbers up to 2 x 12.
For the answers 32 and 40 we thought the factors were 8x4 to make 32 and 8x5 to make 40. However we'd already used the 5x table in another column so we had to change the factors so that 4x8=32 and 4x10=40.
A learning point for all of us was when we discovered that the only way to make 49 was using 7x7. Then we knew we couldn't use any other number twice. From that we could work out that 7x 6=42.
Once we discovered all of the factors, we worked out all of the multiples!
Deniz, Kyristian, Paul, Hamza from Lillington Primary School sent in the following:
We solved this problem by working systematically.
The first thing we looked at was the number 49. The factors for 49 are 1, 49 and 7. The only one we could use was 7 so we knew that the row and column with 42 in had to be 7. This also meant that no other number could be repeated from now on. Looking at the bottom row we now knew this had to be 6 as 6 x 7 = 42.
Secondly we looked at 15 which had to be 3x5. The row had to be 3 and the column 5 as 27 is not in the 5 times table. Using this we knew the last column was 9 because 3x9=27.
Looking down the column with 22 and 24 in tells us this had to be the 2x table meaning the corresponding rows were 11 and 12.
We now only have 8, 4 and 10 left. 40 is the only number in the 10x table and so 10 has to be the column title as the row also contains 32 which isn't in the 10 times table. 10x4=40 so 4 had to be the row. This left 8 to fit in perfectly to the first column.
We then used the numbers to fill in the remainder of the times-table facts.
It was really good to hear about your different approaches, thank you for your well explained solutions.