Freedom and constraints

Combining lengths

Combining rods

The diagrams below show how you can use rods of lengths 3, 4 and 6 units to measure some lengths

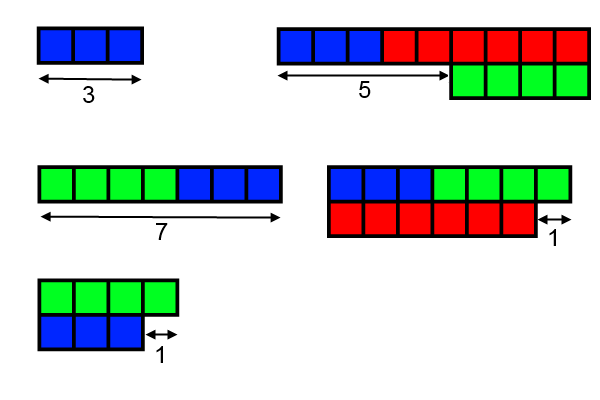
This set of three rods is special because you can measure all the whole number lengths from 1 to 7 units

The diagrams above show how to make lengths of 1, 3, 5 and 7.

There are rods for 4 and 6. Can you see how to make 2?

Can you convince yourself you cannot make 8?

Can you find another set of three rods that can be used to measure all the lengths from 1 to 7? What about 1 to 8? 1 to 9? 1 to ...?

How far can you go?

Once you've had a chance to think about the last question in previous section, watch Alison's and Charlie's video

Alison's video

Charlies's video

What other interesting mathematical questions can you think of to explore next?

Our questions

Is there only one set of three rods that allows you to measure the largest number of consecutive lengths?

What if you could use a set of four rods?...

Is there a way to decide how long the rods should be for any set of rods?

Is there a quick way to work out how far a set of rods will allow you to measure?

What would happen if you could only add lengths together, and couldn't subtract?

A World Without Ones

"Why do we have 1p and 2p coins? There's nothing that only costs a penny or tuppence these days!"

"We need them, to make sure we can make all of the bigger amounts!"

"Well couldn't we do that with some bigger coins?"

"If we only had 3p and 7p coins, there'd be some values that we couldn't make, like 4p or 8p!"

"Yes, but I reckon we'd be able to make most amounts, even if we only had 3p and 7p coins..."

Which values is it impossible to make with 3p and 7p coins?

Is there a point after which you can make every amount?

Given an amount, is there a quick way to work out how to make it?

Is there a quick way to work out the point after which every value can be made?

Are there any pairs of coins where there are infinitely many values that can't be made?