A triomino is a shape made from three squares. Here is an L-triomino:

Here is a size 2 L-triomino:

It can be tiled with four size 1 L-triominoes:


 
Can you work out how to use the tiling of a size 2 L-triomino to help you to tile a size 4 L-triomino? Click here for a hint.

Devise a convincing argument that you will be able to tile a size 8, 16, 32... $2^n$ L-triomino using size 1 L-triominoes.
 
How many size 1 L-triominoes would you need to tile a size 8... 16... 32... $2^n$ L-triomino? 
  
 
What about odd sized L-triominoes? The diagram below shows the region which needs to be tiled to turn a size 1 L-triomino into a size 3 L-triomino.
Can you find a quick way of tiling the region, using combinations of the 'building blocks' below?

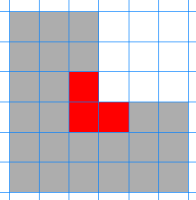
In the same way, can you find a way of adding to your size 3 tiling to tile a size 5? Then a size 7, 9, 11...? Click here for a hint.
Devise a convincing argument that you will be able to tile any odd sized L-triomino using size 1 L-triominoes. 
 
Combine your ideas to produce a convincing argument that ANY size of L-triomino can be tiled.

Here is an interactive you could use to try out your ideas.