Here is a pattern I made with some graphs of trigonometric functions.You can find a copy to print here.

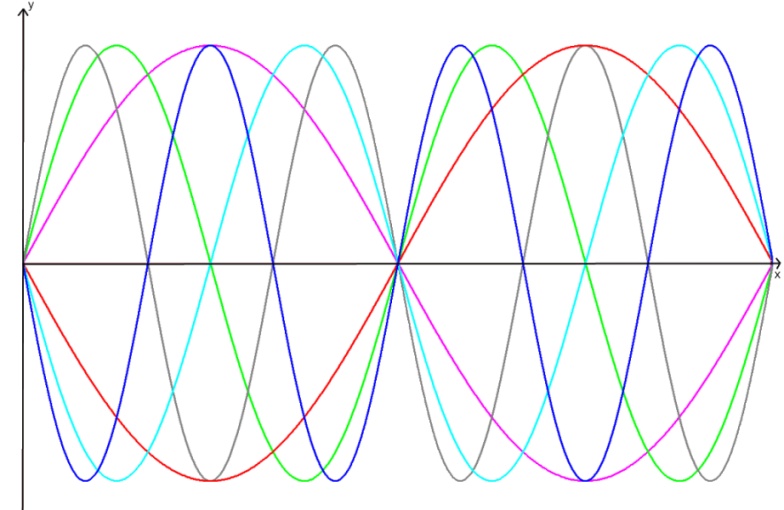
• The purple line is the graph $y=\sin x$. Can you identify the coordinates of the points where it crosses the axes and where it reaches its maximum and its minimum values?

• How could I make the red graph from the purple graph? Can you work out the equation of the red graph?

• The green graph has equation $y=\sin 2x$. Can you describe how to make the green graph from the purple graph? How does the transformation of the graph relate to the way the equation has changed?

• Using these ideas, can you work out the equations of the other graphs I have drawn?

Imagine you had a graphical calculator but the sine button is broken. Can you draw the same patterns using the cosine function instead? Explain how you can transform a cosine graph into a sine graph.

Why not create some trig patterns of your own using graphical calculators or graphing software, and send them to us.
 
This problem is also available in French: Trigo tricoté