Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tangled Trig Graphs
Age 16 to 18
Challenge Level 





Tangled Trig Graphs printable sheet
Here is a pattern I made with some graphs of trigonometric functions.You can find a copy to print here.
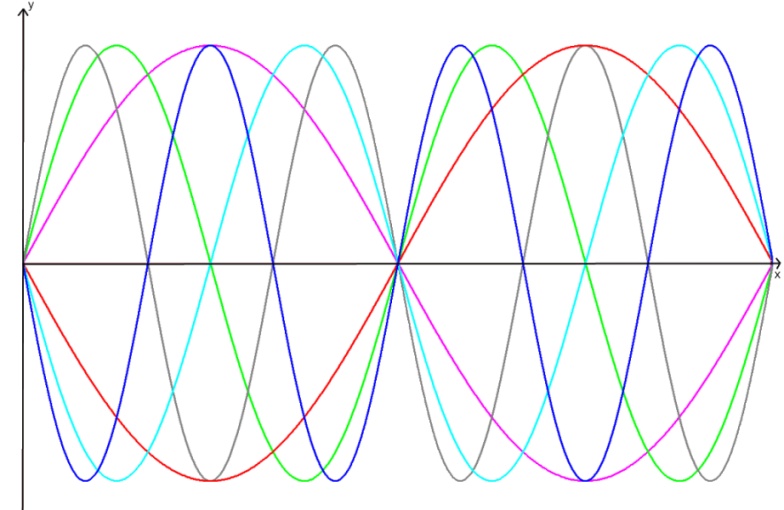
- The purple line is the graph $y=\sin x$. Can you identify the coordinates of the points where it crosses the axes and where it reaches its maximum and its minimum values?
- How could I make the red graph from the purple graph? Can you work out the equation of the red graph?
- The green graph has equation $y=\sin 2x$. Can you describe how to make the green graph from the purple graph? How does the transformation of the graph relate to the way the equation has changed?
- Using these ideas, can you work out the equations of the other graphs I have drawn?
Imagine you had a graphical calculator but the sine button is broken. Can you draw the same patterns using the cosine function instead? Explain how you can transform a cosine graph into a sine graph.
Why not create some trig patterns of your own using graphical calculators or graphing software, and send them to us.
This problem is also available in French: Trigo tricoté
You may also like
Small Steps
Two problems about infinite processes where smaller and smaller steps are taken and you have to discover what happens in the limit.