Fractional Triangles

'Fractional Triangles' printed from https://nrich.maths.org/

Show menu

Fractional Triangles

Use the lines on this figure to show how the pattern of triangles can be used to divide the square into two halves, three thirds, six sixths and nine ninths.

More lines are needed to divide it into four quarters.

What is the least amount of line needed to do this if the quarters are in one piece and all the same shape?

How many ways can you divide it into halves using just the lines given?

Why do this problem?

This problem could be used as part of a lesson on finding fractions of various shapes. It should help develop an understanding of the relationship between the part and the whole. It allows children to explore fractions in a non-threatening, open-ended way and yet it does contain some real challenge.

Possible approach

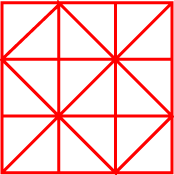
The problem could be introduced by showing the design to all the group. You could either draw it on the board or display this image on an interactive whiteboard. Alternatively, you could print out this sheet (enlarged to A3 if required). Whichever way you decide, it would be good if the image could be annotated by children during the lesson.

Ask the children what they can see and invite them to talk about it - think, pair, share. You could steer the conversation towards numbers and fractions if the children do not naturally bring it up. Asking general questions about the numbers and fractions of different shapes in the design will give children the confidence to tackle the problem.

This sheet (which contains six copies of the image) could be used both to work on and record answers to the problem. Coloured pencils would be useful to emphasise the different shapes within the design.

The final question in the problem: "How many ways can you divide it into halves using just the lines given?" could provide a useful starting point for a plenary as even those who have had difficulty with some of the questions could join in usefully.

Key questions

What fraction of the design are the small squares?

How many sixths are there in a third?

Possible extension

Children could explore the design further and find the fraction of other shapes within the design such as the diagonally placed squares formed by four small triangles.

Possible support

Those experiencing difficulty with this problem may find it easier to start by looking at a $3 \times3$ grid. Even if the rest of the class are not using it, this sheet could be useful. Some learners may find it helpful to cut out the different fractions of the square to check that they are identical. (If this is the case, several copies of the image will be needed!)