Andaleeb sent in this excellent solution.

The diagram shows some of the vertical lines drawn for values of x between 0 and 1 as described in the question. The lines are of height 1 unit at x = 0 and 1, of height ${1\over 2}$ units at $x= {1\over 2}$ , of height ${1\over 4}$ units at $x= {k\over 4}$ and ${1\over 8}$ units at $x= {k\over 8}$ and so on... up to ${1\over 2^5}$ at ${k\over 2^5}$ where $k$ is a positive integer.

n	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$\dots$	$n$	$n+1$
Height	$1$	${1\over 2}$	${1\over 4 }$	${1\over 8}$	${1\over 16}$	${1\over 32 }$	${1\over 64}$	$\dots$	${1\over 2^n}$	${1\over 2^{n+1`}}$
Lines cut	$2$	$1$	$2$	$4$	$8$	$16$	$32$	$\dots$	$2^{n-1}$	$ 2^n$

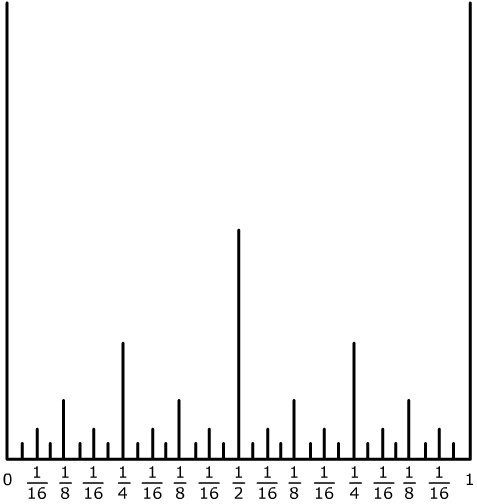
Thus if the height $h$ lies in ${1\over 2^n} > h> {1\over 2^{n+1}}$ then the number of lines cut is given by $$ 2 + 1 + 2 + 4 + 8 + ... + 2^{n-1} = 2 + {{2^n - 1} \over {2 - 1}} = 2^n + 1.$$ As $n$ tends to infinity the height of the lines tends to 0 and the number of lines cut tends to infinity.