Route product
Find the product of the numbers on the routes from A to B. Which route has the smallest product? Which the largest?
Problem
There are lots of different routes from $A$ to $B$ in this diagram:
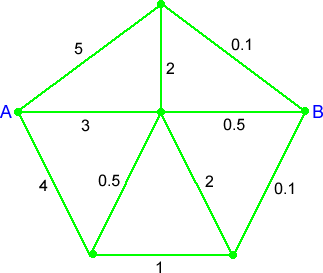
Details
For accessibility: A pentagon with a line joining each corner to a point in the centre. The vertex on the far left is labelled A and the vertex on the far right is labelled B. From A to the top vertex is labelled 5. From the top vertex to B is labelled 0.1. From the top vertex to the centre vertex is labelled 2. From A to the centre vertex is labelled 3. From B to the centre vertex is labelled 0.5. From A to the bottom left vertex is labelled 4. From the bottom left vertex to the centre is labelled 0.5. From B to the bottom right vertex is labelled 0.1. From the bottom right vertex to the centre is labelled 2. From the bottom right vertex to the bottom left vertex is labelled 1.
The idea is to work out the product of the numbers on these different routes from $A$ to $B$. Let's say that in a route you are not allowed to visit a point more than once.
For example, we could have $3\times0.5$ but we couldn't have $3\times2\times5\times4\times1\times 0.1$ because that route passes through $A$ twice.
Which route or routes give the largest product?
Which route or routes give the smallest product?
Do you have any quick ways of working out the products each time?
[This problem is adapted from a SMILE Centre card.]
Getting Started
Can you see immediately which routes might have large products and which ones small products?
How will you know that you have checked all the routes?
How many routes can you find which use the $5$? What is the product of each one?
How many routes use the $3$? And the $4$?
Student Solutions
Neil from Kells Lande Primary School wrote to say:
The route with the largest product is going up from A along the $5$ line, and down along the $2$ line, and then along the $0.5$ line to B, which has a product of $5$.
The route with the smallest product is to go horizontally along the $3$ line from A, then down the first $0.5$ line, along the $1$ line going horizontally, and then up to B along the $0.1$ line, which has a product of $0.15$.
You're right, well done, Neil. Class K's Magic Mathematicians at Charter Primary School told us how they found out the solution:
We worked in a group of four and found out all the routes from A to B, then we did all the sums and worked out all the answers.
Many of you also said that to find the largest and smallest products, it helped to look for the largest and smallest numbers. That's a good strategy, well done.
Teachers' Resources
Route Product
There are lots of different routes from $A$ to $B$ in this diagram:
The idea is to work out the product of the numbers on these different routes from $A$ to $B$. Let's say that in a route you are not allowed to visit a point more than once.
For example, we could have $3\times0.5$ but we couldn't have $3\times2\times5\times4\times1\times 0.1$ because that route passes through $A$ twice.
Which route or routes give the largest product?
Which route or routes give the smallest product?
Do you have any quick ways of working out the products each time?
[This problem is adapted from a SMILE Centre card.]
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support