Golden eggs
Find a connection between the shape of a special ellipse and an
infinite string of nested square roots.
Problem
Image
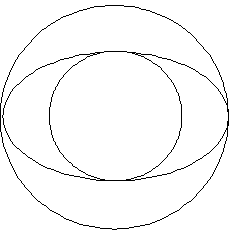
1) An ellipse with semi axes $a$ and $b$ fits between two circles of radii $a$ and $b$ (where $b> a$) as shown in the diagram. If the area of the ellipse is equal to the area of the annulus what is the ratio $b:a$?
(2) Find the value of $R$ if this sequence of 'nested square roots' continues indefinitely: $$R=\sqrt{1 + \sqrt{1 + \sqrt {1 + \sqrt {1 + ...}}}}.$$
Getting Started
(1) You will need to know, or find out, the formula for the area of an ellipse. All you have to do then is solve a quadratic equation.
(2) What happens if you square this strange expression?
Student Solutions
Congratulations Joseph from Colyton Grammar School, Adam from the University of Waterloo, Shaun from Nottingham High School and Andrei from Tudor Vianu National College, Bucharest, Romania for your solutions.
(1) If the area of the ellipse equals the area of the annulus then $\pi ab = \pi b^2 - \pi a^2$ and so $ab = b^2 - a^2 $. Then, dividing by $a^2$, $$ b/a = (b/a)^2 -1.$$ The ratio we want to find is $b/a$, the ratio of the longer to the shorter axis of the ellipse. So let $b/a = x$ then $$x^2 - x - 1 = 0.$$ Using quadratic formula: $$x = {1\pm \sqrt 5 \over 2}$$ We choose the positive root knowing that the ratio $b/a$ is positive so this ratio is equal to the golden ratio.
(2) Note that $R$ appears itself in the nested root. Therefore we can say $$R = \sqrt (1 + R)$$ and so $$ R^2 - R - 1 = 0.$$ We have a quadratic of the same form as above. Hence we find $R$ to be the golden ratio.
Teachers' Resources
The second part of this question introduces an expression involving an infinite string of nested square roots but, as forbidding as it may seem, a little ingenuity is all that is needed to evaluate it.
