Smashing Time
Once granny has smashed some of her cups and saucers, how many cups are now without saucers?
Problem
Yesterday, Granny had 12 cups and 10 matching saucers, but this morning she dropped a tray holding one third of the cups and half the saucers, breaking all of those on the tray.
How many of her cups are now without saucers if...
a) all of the cups are identical, and all of the saucers are identical?
b) the cups are all different to each other, and 10 of the cups matched a specific saucer?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Answer: a) 3
a) 12 cups $\rightarrow$ lose one third = 4
$\therefore$ 8 cups left
10 saucers $\rightarrow$ lose half = 5
$\therefore$ 5 saucers left
8 $-$ 5 = 3
$\therefore$ 3 cups do not have matching saucers.
Answer: b) 3, 4, 5, 6 or 7
b) Represent the 12 cups and 10 saucers as being different colours:
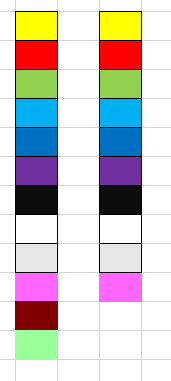
If the 4 cups smashed are the bottom 4 and the 5 saucers smashed are the bottom 5 (for example), then there are 3 cups without matching saucers.
If the 4 cups smashed are the top 4 and the 5 saucers smashed are the bottom 5 (for example), then there are 7 cups without matching saucers (see below).

Thank you to Luke from Lode Heath School for proposing and solving part (b) of this problem
