Sitting Pretty
Problem
Sitting Pretty printable sheet
A circle 'sits' on a right-angled triangle, touches two sides of the triangle and has its centre on the hypotenuse of the triangle. The circle has radius $r$ and the triangle has sides of length $x$ and $y$.
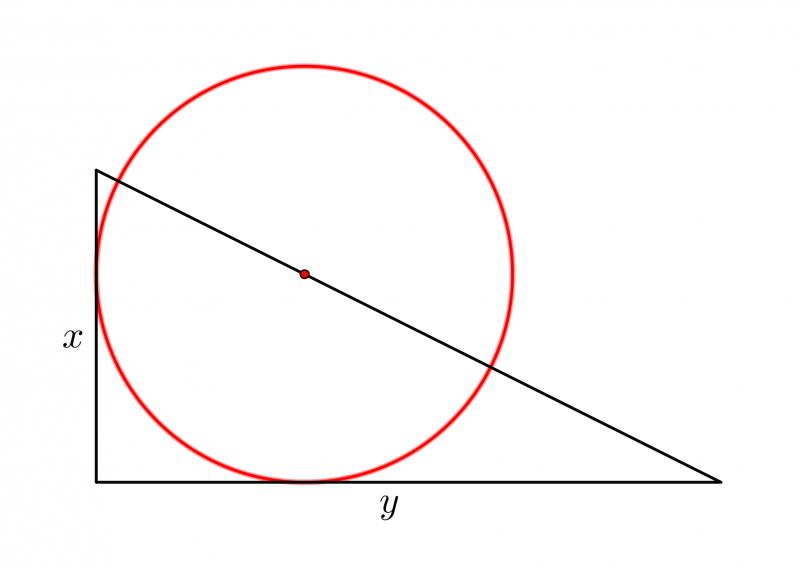
Show that $\dfrac{1}{r} = \dfrac{1}{x} + \dfrac{1}{y}$.
Getting Started
Does this give you any similar triangles?
Student Solutions
We received many good solutions of this question. They either use the properties of the area of triangles or similar triangles to solve the problem.
Emile from CNDL and John from South Island School (Hong Kong) used the area of triangles to solve the problem. Emile writes:
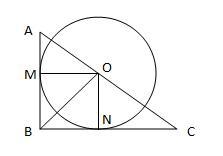
$xy/ 2$ is the area of the triangle ABC. You can also divide the triangle in to two triangles AB and CBO with area $rx/2$ and $ry/2$ respectively. Thus, we have
$$xy/2=rx/2+ry/2\;.$$ Thus,
$$
\begin{align}
xy&=rx+ry\\
xy&=r(x+y)\\
1/r&=(x+y)/xy\\
1/r&=1/x+1/y\;.\\
\end{align}
$$
Rachel, Emily, Samantha and Kri from Millais School, Ciaran from St Patrick's School, Wilson's School Maths Club and Nathanael used similar triangles to solve this problem. This is the solution from Ciaran of St Patrick's school.
AB and BC are tangents to the circle, thus ON and OM are perpendicular to BC and AB. Thus triangle ONC and triangle ABC are similar since they share the same angle C and both have a right angle. $ON = r$ and $NC = y-r.$ Thus,
$$
\begin{align}
r/(y-r) &= x/y\\
ry &= xy -rx\\
ry + rx &= xy\\
xy&=r(x+y)\\
1/r&=(x+y)/xy\\
1/r&=1/x+1/y
\end{align}
$$
and the rest of the solution is the same as Emile's.
Congratulations to all of you who did it correctly.
Teachers' Resources
Why do this problem :
This problem offers students a valuable context in which to visualise the effect of constraints (the fact that the centre of the circle is on the hypotenuse). They can be encouraged to establish the relationships within the context (for example by utilising properties of similar triangles), and then find a way to use those to make a route to a solution, which might include working backwards as well as algebraic manipulation.
Possible approach :
This printable worksheet may be useful: Sitting Pretty
Invite the group to visualise the circle, perhaps rolling into place. Draw attention to its size and position and identify the constraints under which this circle exists.
You might wish to invite learners to try fixing the radius of the circle (at 3cm say) and constructing triangles around it.
- What possible values can x and y have and does the relationship hold in these cases?
- Do they notice anything about the relationship between x and y?
- How many possible values of x and y can there be, and does the relationship hold for any of them?
Ask students to create their own diagram. The questions below at the right moment may help to steer the thought process with a light touch. Adding lines that represent the constraints of the situation will be helpful, so students must feel free to redraw their diagrams until they are happy that they have arrived at a good representation.
Key questions :
- Look at your diagram, what's there that might help ?
- What's there anyway ?
- Paying attention to any triangles in your diagram, what do you think about the relationship between them. What might be true ?
- Is it ? Why ?
- How might that help ?
- What is it that this problem asks us to find out ?
Possible support :
Some students might not immediately be ready for this because they are not sufficiently familiar with the similar triangle context, but it is more likely that the algebra demand is too great. It may be that this problem works well as a 'guided example' where the teacher still asks questions, and shares the 'blocks', which at each point need to be identified and a way ahead sought, but takes the group on a pre-determined journey to the solution. Perhaps asking learners to work with some real values to explore possibilities and verify the relationship for these cases.
Possible extension :
Partly Circles is another challenging problem where students can apply their understanding of circle geometry.
