Let Us Reflect
You will need a mirror for this activity.
Here is a square:
Where can you put the mirror across the square so that you can still 'see' the whole square?
How many different positions are possible?
How many lines of symmetry does a square have?
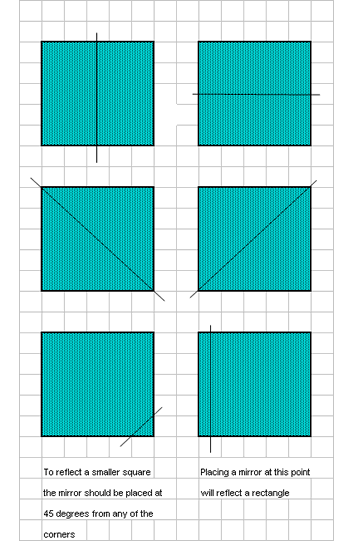
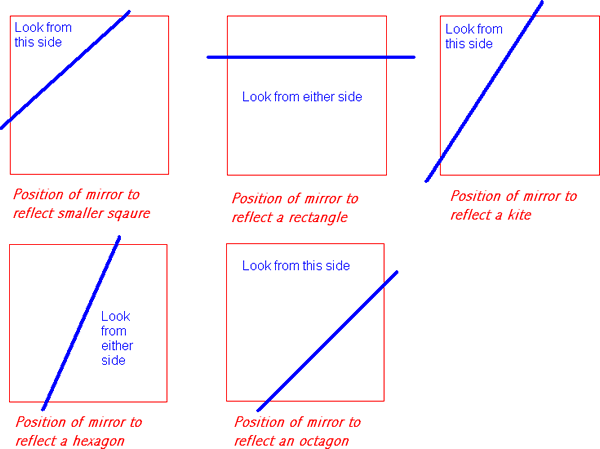
Can you reflect part of the square so that you can see a smaller square?
A rectangle? A kite? A hexagon? An octagon?
What do all the shapes have in common?
This problem has been adapted from the book "Starting from Mirrors" by David Fielker, published by BEAM Education. This book is out of print but can still be found on Amazon.
You might find it useful to print off this sheet of squares.
Try experimenting by placing the mirror across the middle of the square to start with then move it gradually in one direction to see what happens.
Try a different starting position now - perhaps still across the middle, but at a different angle.
Ruth has sent in some ideas for the first part of the question. She says you can put a mirror across the middle or diagonally from corner to corner to see the whole square. She sent these diagrams:
|
Image
|
Image
|
Thank you for writing to us Siobhan, Ruth and Gemma. Well done!
Let's Reflect
You will need a mirror for this activity.
Here is a square:
Where can you put the mirror across the square so that you can still 'see' the whole square?
How many different positions are possible?
How many lines of symmetry does a square have?
Can you reflect part of the square so that you can see a smaller square?
A rectangle? A kite? A hexagon? An octagon?
What do all the shapes have in common?
This problem has been adapted from the book "Starting from Mirrors" by David Fielker, published by BEAM Education. This book is out of print but can still be found on Amazon.