Harmonic triangle
Can you see how to build a harmonic triangle? Can you work out the next two rows?
Problem
Harmonic Triangle printable worksheet
This is the start of the harmonic triangle:
\begin{array}{ccccccccccc} & & & & &\frac{1}{1} & & & & & \\ & & & & \frac{1}{2} & & \frac{1}{2} & & & & \\ & & & \frac{1}{3} & &\frac{1}{6} & & \frac{1}{3} & & & \\ & & \frac{1}{4} & &\frac{1}{12} & & \frac{1}{12} & & \frac{1}{4} & & \\ & \frac{1}{5} & & \frac{1}{20} & & \frac{1}{30} & & \frac{1}{20} & & \frac{1}{5} & \\ \frac{1}{6} & & \frac{1}{30} & & \frac{1}{60} & & \frac{1}{60} & & \frac{1}{30} & & \frac{1}{6}\\ & & & & & \ldots& & & & & \end{array}
Each fraction is equal to the sum of the two fractions below it.
Look at the triangle above and check that the rule really does work.
Can you work out the next two rows?
The $n$th row starts with the fraction $\frac{1}{n}$, so the first diagonal goes:
$\frac{1}{1}$, $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{4}$...
Take a look at the second diagonal:
$\frac{1}{2}$, $\frac{1}{6}$, $\frac{1}{12}$, $\frac{1}{20}$...
Can you see a pattern?
What fraction will appear in the second position on the nth row?
Can you prove it?
What about the third and fourth diagonals?
Click here for a poster of this problem.
Getting Started
$$\frac{1}{2} = \frac{1}{3} + \frac{1}{6}$$
$$\frac{1}{3} = \frac{1}{4} + \frac{1}{12}$$
$$\frac{1}{12} = \frac{1}{20} + \frac{1}{30}$$
Look at the diagonal lines running from the right down to the left. The fractions in the first one are $\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}$ and so on.
If $\frac{1}{n}$ is at the end of the nth row, the fraction above it must be $\frac{1}{n-1}$ and the fraction below it must be $\frac{1}{n+1}$.
Have a look at the second diagonal (the one formed by taking the second number in each row: it starts $\frac{1}{2}, \frac{1}{6}, \frac{1}{12}, \frac{1}{20}$.
Can you find a pattern for these numbers so that you can work them out easily (without having to subtract fractions)?
Can you explain why the pattern works?
Student Solutions
Congratulations to Alice who sent in a correct solution to this problem:
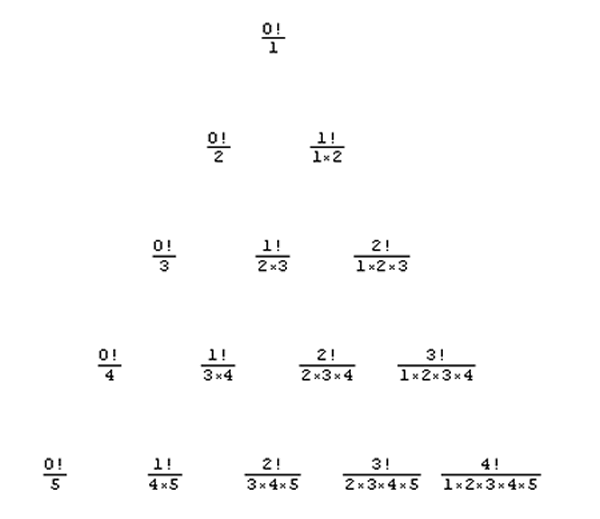
Congratulations to Ray who also worked on this problem and sent us the following result:
Teachers' Resources
Why do this problem?
This problem provides a fraction-based challenge for students who already possess a good understanding of fraction addition and subtraction, and it leads to algebraic manipulation of that same process.
Possible approach
This printable worksheet may be useful: Harmonic Triangle.
Silently, and with the full class attention (!) begin writing the triangle on the board, slowly, row by row. Students can put up hands when they know what is coming next. Allow whispered explanations, until everyone seems to have some idea, then invite explanations from students.
In pairs let students generate as much of the pyramid array as they can.
Bring the group together and ask about what is easy/hard, and any short cuts/observations anyone has made. Suggest that students work on one diagonal at a time, and redefine their task as finding, and trying to prove, general methods for calculating numbers in this table, (for example, can they establish the second number in the $46$th row? The nth row? What about the third numbers?).
Note : How far this problem goes will depend on the confidence students have at using algebra to represent and explore generality. The general term in the second diagonal should be accessible to most students who can manage algebraic fractions and many who can't but who can reason generally based on the patterns in the numerical values.
There is no rush to finalise a proof for any term in the array, the algebra involved isn't completely simple and the reasoning based on the algebra needs to be thorough. But this is an excellent context in which to sense generality while proof requires some care and imagination.
Key questions
- What's the reason why your pattern must continue? How sure are you?
- Try to find the first case where it doesn't work.
- If you think it will continue indefinitely, can that be proved?
Possible support
Learners might find it useful to use these cards to recreate the triangle as a group activity. There are a few fractions missing and the blank cards can be completed to fill in the gaps.
An alternative, easier task working with unit fractions is Egyptian Fractions
This could be a replacement for, or a preliminary to Harmonic Triangles.
Gordon Davis, who teaches at Colyton Grammar School in Devon, UK said:
"After introducing the structure of the triangle briefly, I gave groups sugar paper and slips of paper with all the fractions that they would need for the first seven rows of the triangle. There was a massive amount of mental calculation, as students organised and stuck down their fractions.
It worked well as there was a lot of space on the sugar paper for students to note down any observations they had. I asked them to highlight any of these comments that they could prove to be true always.
We then spent most of the lesson trying to establish the terms on the 100th row."
Possible extension
Press students to justify their conjectures using algebraic reasoning, extended gradually to cover all terms across a row.
