Geoboards
This practical challenge invites you to investigate the different
squares you can make on a square geoboard or pegboard.
Problem
| On a $4$ by $4$ geoboard (say) - how many different sized squares can you make using rubber bands? How could you make a square with NO pins along a side (an edge) and just the 4 pins at the corners (vertices)? The basic unit of measurement is one square unit (as shaded in the diagram). How can you make a square whose area is 2 square units? Can you make a square with an area of 3 square units? |
Image

|
Here is an interactive you might like to use.
Getting Started
Try starting a square on one of the edge pegs. Look at
all the other pegs in turn - could you use that peg as the second
corner of a square?
Can you make a square whose edges aren't parallel to the rows or columns of pegs?
Can you make a square whose edges aren't parallel to the rows or columns of pegs?
Student Solutions
Geraldine and Suzanne sent in their solutions to this problem. They said:
We think there are five different squares which you can make on a 4 by 4 geoboard. Here is a picture of three of them:Image
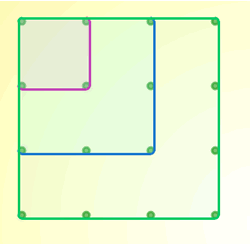
Here is a picture of the other two which only have pegs at their corners, not along their sides:
Image
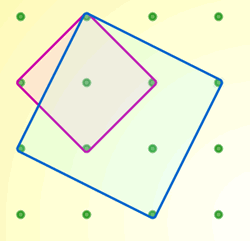
The pink square in the second picture has an area of two square units. We don't think you can make a square with an area of three square units as the next size up square we have has sides of 2 which means its area is 4 square units (too big).
Teachers' Resources
This problem is written to stimulate exploration on a geoboard and the hope is that you and your pupils will find further questions to investigate.
The problem is a nice way of raising pupils' awareness of "tilted" squares on a grid and of challenging the frequently-heard cry of "but that's a diamond"! It would be interesting to set children off on tackling this problem, perhaps in pairs, and to listen to the discussion which follows. If, after a short time, no-one has found a tilted square, you could cut out a square from paper, and, after ascertaining from the class what shape it is, you could stick it on the board in different orientations, asking each time whether the shape has changed.
Having found all the different squares, investigating their areas is a natural follow-up which is made accessible by the grid itself.
