First Forward into Logo 7: Angles of Polygons

More Logo for beginners. Learn to calculate exterior angles and draw regular polygons using procedures and variables.
Age
11 to 18
Challenge level
filled star empty star empty star
Exploring and noticing Working systematically Conjecturing and generalising Visualising and representing Reasoning, convincing and proving
Being curious Being resourceful Being resilient Being collaborative

Problem

First Forward Into Logo

Previous: FF6

 

In FF6 you considered and hopefully explored the following procedures:

TO CIRCLE :CH

REPEAT 360 [ FD :CH RT 1]

END

TO CIRC :CH :ANG

REPEAT 360 [ FD :CH RT :ANG]

END

As a consequence different sized circles and some polygons may have resulted. Did any of you manage to draw a heptagon ($7$- sided)? A nonagon ($9$-sided)? A endecagon($11$- sided)? $13$-gon? Etc. etc....

Imagine walking around the outside of a pentagon....as you: go forward then turn, go forward then turn, go forward then turn, go forward then turn, ... finally go forward then turn. You should be back where you started... go on try it, convince yourself. In your journey you should have turned through $360^\circ$ .

Five times you turned through $72^\circ$ . N.B. $5 \times72 = 360$.

 

Hence:


For a pentagon - REPEAT 5 [ FD 45 RT 360/5]
For a heptagon - REPEAT 7 [FD 45 RT 360/7]
For a nonagon - REPEAT 9 [ FD 45 RT 360/9]
First Forward into Logo 7: Angles of Polygons


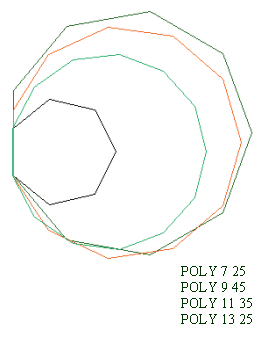
See the pattern?

So why not experiment?

Go on try:

TO POLY :N

REPEAT :N [FD 45 RT 360/:N]

END

Then try:

TO POLY :N :M

REPEAT :N [FD :M RT 360/:N]

END

 

Next: FF8