Cyclic Quadrilaterals Proof
Can you prove that the opposite angles of cyclic quadrilaterals add to $180^\circ$?
Problem
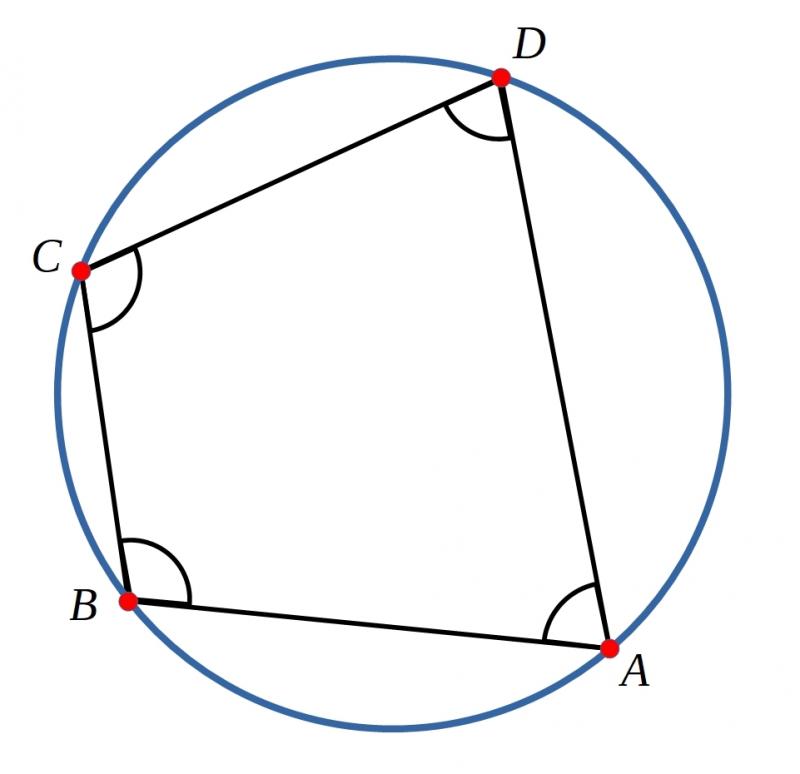
This problem follows on from Cyclic Quadrilaterals
Sketch a circle and choose four points at random to form a quadrilateral.
Can you prove that the opposite angles of your quadrilateral add to $180^\circ$?
Click below to see a diagram that might help you to prove it.
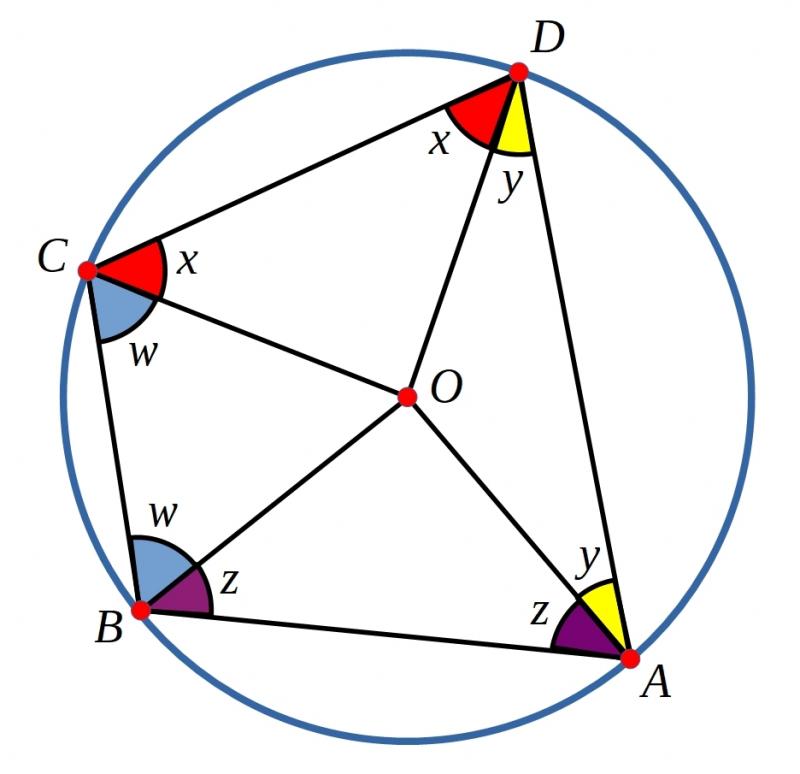
Quadrilaterals whose vertices lie on the edge of a circle are called Cyclic Quadrilaterals.
Extension

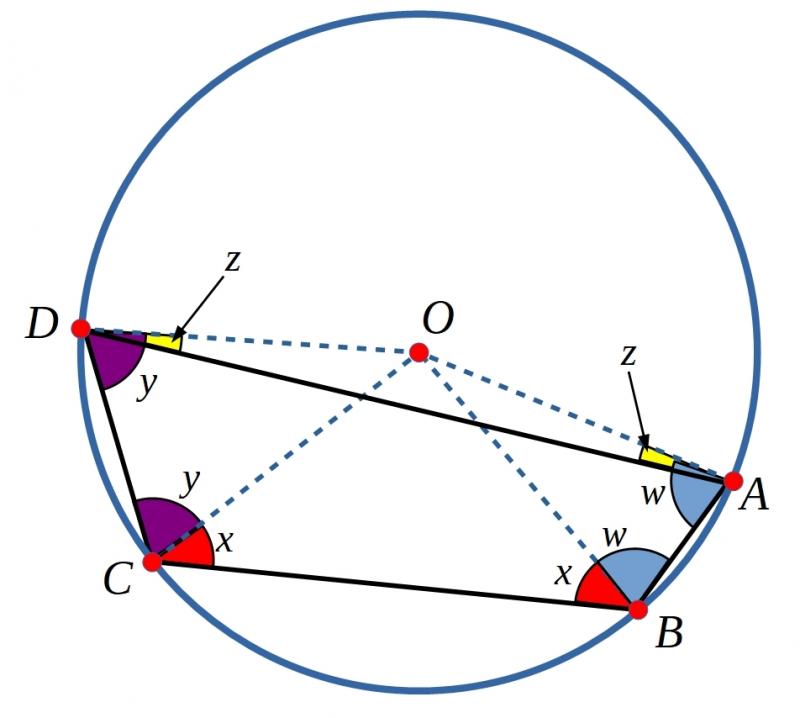
Can you prove that when the centre of the circle is outside the cyclic quadrilateral, the opposite angles also add to $180^\circ$?
You may wish to draw some examples on
9, 10, 12, 15 and 18 dot circles.
Click below to see a diagram that might help you to prove that the opposite angles of cyclic quadrilaterals add to $180^\circ$, when the centre of the circle is outside the cyclic quadrilateral.
You may be interested in the other problems in our Sharpen your Skills Feature.
Getting Started
Start by taking a look at Cyclic Quadrilaterals
You can use the Geogebra app below to try to explore opposite angles in a cyclic quadrilateral before trying to prove the result.
Student Solutions
Sunhari from British School Muscat in Oman and Rohan form Wilson's School in the UK used the same method to prove that opposite angles in a cyclic quadrilateral add up to 180$^\circ$ (assuming the centre of the circle is inside the quadrilateral). This is Sunhari's work (click on the image to see a larger version):

Nayanika from The Tiffin Girls' School Theo from Pate's School in the UK used a different method. This is Theo's proof:

$A+B+C+D$ must equal $360$ as the angles form a quadrilateral. You can also write this as:
$2w+2x+2y+2z = 360$
$2(w+x+y+z) = 360$
$w+x+y+z = 180$
Two opposite angles will compose of all four different variables once, so the two opposite angles will add up to $180.$
For the extension - proving that the opposite angles still add up to 180$^\circ$ even if the centre of the circle is outside the quadrilateral - Neel from Zurich International school in Switzerland sent in this example. Note that Neel has proved that it has worked for one cyclic quadrilateral, but not for all possible cyclic quadrilaterals.
This is Nayanika's proof (similar to Theo's proof above) (click on the image to see a larger version):

This is Rohan's proof (similar to Sunhari's proof above):



Teachers' Resources
Why do this problem?
Working on this problem leads students to an accessible proof that opposite angles in a cyclic quadrilateral sum to $180^\circ$.
Possible approach
This problem follows on from Cyclic Quadrilaterals
“Well we haven't found any examples where the opposite angles don't add up to 180 degrees, but that doesn't mean it will always work - I wonder if we can prove it?”
“Take a look at this diagram and try to come up with a convincing argument that the opposite angles in a cyclic quadrilateral will always add up to 180 degrees.”

Give students some time to think about a proof. Circulate and look out for students who notice that:
two yellows + two purples + two blues + two reds = 360 degrees
so, one yellow + one purple + one blue + one red = 180 degrees
or
$2w + 2x + 2y + 2z = 360^\circ$
so, $w + x + y + z = 180^\circ$
Opposite angles contain one yellow, one purple, one blue and one red (or one $w$, one $x$, one $y$ and one $z$), so opposite angles add up to 180 degrees.
Bring the class together to share their thoughts.
Possible extension
Challenge students to consider whether the opposite angles of cyclic quadrilaterals add to $180^\circ$, when the centre of the circle is outside the cyclic quadrilateral.
Other circle theorems, and an alternative proof to the one suggested in this problem, can be explored in Circumference Angles
The Geogebra app below might be helpful when exploring opposite angles.
