Circumference angles
Can you prove the angle properties described by some of the circle theorems?
Problem
Circumference Angles printable sheet - proof sorter
Circumference Angles printable sheet - corollaries
Try moving the points $A$, $B$ and $C$ around (but keep them in the order $A, B, C$ going clockwise!).
What do you notice about the two angles marked in the diagram?
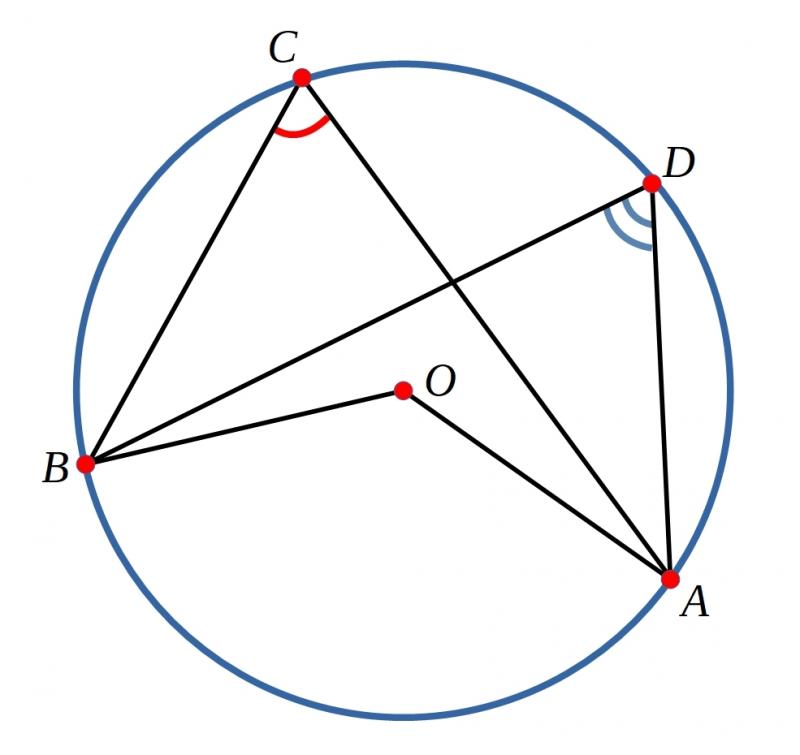
Can you use the diagram below to prove your findings?

You might like to use this Proof Sorter to help you construct a proof.
Having now proved this result, you can use it to show that some other things are also true.
Propositions which follow on from a theorem are sometimes called corollaries.
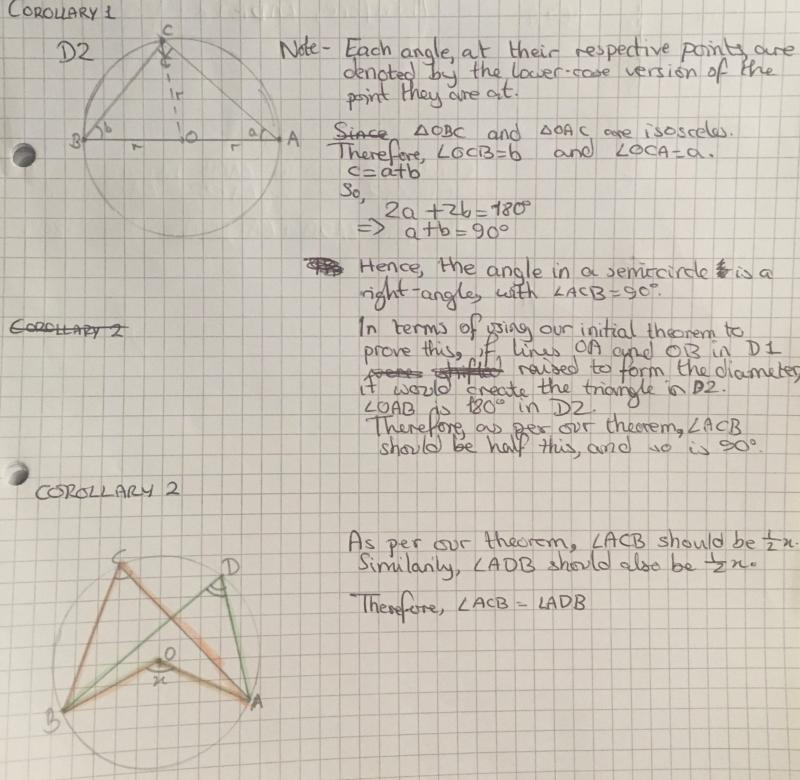
Corollary 1
Can you show that the angle in a semi-circle is a right-angle?
(I.e. if $AB$ is a diameter then angle $ACB=90^{\circ}$.)

Corollary 2
Can you show that the two angles marked in the diagram below are equal?
Corollary 3
Can you show that the two angles marked in the diagram below add up to $180^{\circ}$?

Can you use your results to show that the two angles marked in the diagram below add up to $180^{\circ}$?

Student Solutions
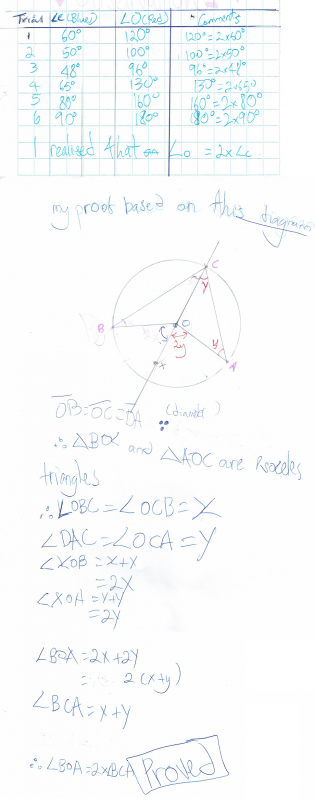
Well done to Ci Hui Minh Ngoc Ong from Kong Hwa School in Singapore, Nayanika from The Tiffin Girls' School and Lewis from Wilson's School, both in the UK, who sent in complete proofs for the original problem.
This is Ci Hui Minh Ngoc Ong's work for the original problem:
Harry from Crestwood Community School, Lewis and Nayanika sent in proofs for corollaries 1, 2 and 3. This is Nayanika's work for corollaries 1 and 2 (click on the image to see a larger version):
Harry proved corollary 2 in a slightly different way. Harry wrote:
Both D and C are connected to A and B, D and C can be moved freely without the angle changing, meaning that they are both the same angle because they are both connected to the same points.
Here is Lewis's proof of corollary 3 (click to see a larger version):

Nayanika and Lewis also proved corollary 4. Here is Nayanika's work (click to see a larger version):

Teachers' Resources
Why do this problem?
This problem introduces the "Angle at the Centre" circle theorem via a Geogebra app. Once students have noticed that the angle at the centre of the circle is double the angle at the circumference, there is a diagram and a proof sorter to help them construct a proof of the theorem.
There are opportunities here to discuss the difference between observations and rigorous proof, and also the opportunity to see how one result can be used to prove other results. In this case, the angle at the centre theorem is used to prove that angles in the same segment are equal, that the angle in a semi-circle is a right-angle, and that opposite angles in a quadrilateral add up to $180^{\circ}$.
Note that if the order of the points $ABC$ is changed to anti-clockwise the geogebra app shows a different angle at the centre. Students could be asked to find a relationship between these two angles as well!
Possible approach
This problem featured in an NRICH Secondary webinar in March 2022.
These printable cards for sorting may be useful: Circumference Angles
Remind students of the key vocabulary of circle (in particular: Centre, Circumference, Chord, Radius)
Project the app onto a white/smart board and move some of the points around.
Ask the class what the angle at the centre would be if the angle at the circumference was $20^{\circ}$ (and similar).
Students could draw some examples using dotty circles, and calculate the angles at the centre and at the circumference (the 9-point and 12-point circles are quite helpful - see Cyclic Quadrilaterals for an idea of how this can be done, and for printable circle sheets).
For the proof, project the diagram, or draw a diagram without marked angles, and ask what sort of triangles they can find. Also ask which angles are the same.
Students can use the interactive proof sorter, or a print out of the statements, and use this to construct a proof.
For the Corollaries, students should be encouraged to think how the circle theorem they have proved can be used to prove these further statements as efficiently as possible.
Key questions
Using the app:
- What do we call the various parts of the circle, and what do we call lines across which do, or do not, pass through the centre of the circle?
- If the angle at the circumference is $20^{\circ}$, what will the angle at the centre be? (And similar)
Proving the result - using the diagram and/or proof sorter
- What can you say about triangles $BOC$ and $AOC$?
- Which angles are equal to each other?
- If $\angle OBC = x$, which other angles can you find in terms of $x$?
- How does $\angle XOB$ compare to $\angle OCB$?
Possible extension
Students can also look at Cyclic Quadrilaterals for an alternative proof of this theorem.
