Cyclic quadrilaterals
Draw some quadrilaterals on a 9-point circle and work out the angles. Is there a theorem?
Problem
Cyclic Quadrilaterals printable sheet
Printable sheets of circles with a central point can be found on our printable resources page.
In the GeoGebra interactivity below there is a circle with 9 equally spaced points on the edge, and one in the centre.
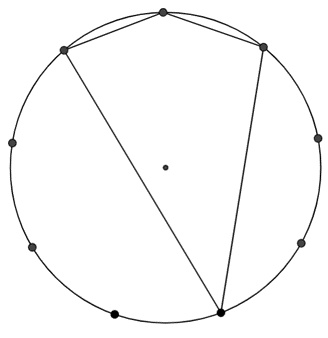
Draw as many different triangles as you can, by joining the centre dot and any two of the dots on the edge.
Can you work out the angles in your triangles?
You should have found four different triangles with angles of:
80, 50, 50
120, 30, 30,
160, 10, 10

Now draw a few quadrilaterals whose interior contains the centre of the circle, by joining four dots on the edge.
Can you work out the angles of your quadrilaterals?
If you're finding it hard to work out the angles, take a look at Getting Started.
Create at least five different quadrilaterals in this way and work out their angles.
What do you notice about the angles on opposite vertices of your quadrilaterals?
Perhaps you are wondering whether this only happens with 9-dot circles...
You may wish to explore the opposite angles of quadrilaterals on circles with a different number of dots.
Click below for interactivities with 10, 12, 15 and 18 dots around the circle.
10 dots
12 dots
15 dots
18 dots
Extension:
Will the same happen if you draw a circle and choose four points at random to form a quadrilateral?
To prove that the opposite angles of all cyclic quadrilaterals add to $180^\circ$ go to Cyclic Quadrilaterals Proof
Quadrilaterals whose vertices lie on the edge of a circle are called Cyclic Quadrilaterals.
You may be interested in the other problems in our Sharpen your Skills Feature.
Getting Started
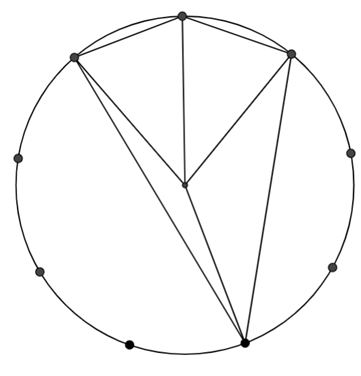
Draw lines from the centre point to the vertices of your quadrilaterals in order to construct some isosceles triangles.
Student Solutions
Can you work out the angles in your triangles?
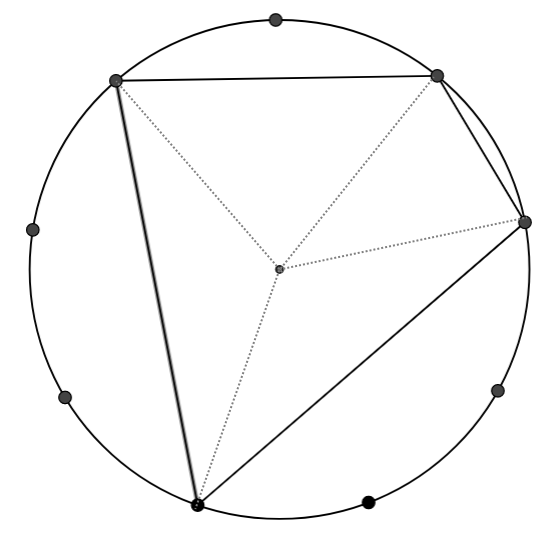
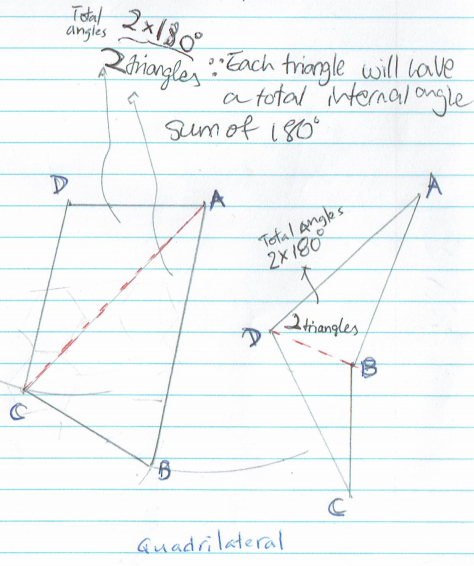
Dan, Taylor, Grace and Summer from Long Field Spencer Academy in England, Ci Hui from Queensland College of Science and Technology in Australia, Thomas and Justin from Daegu International School in South Korea and Shaunak from Ganit Manthan, Vicharvatika in India worked out the angles in their triangles. Dan described a general method:

This is Ci Hui's work finding the angles in all of the possible triangles, using the same method:
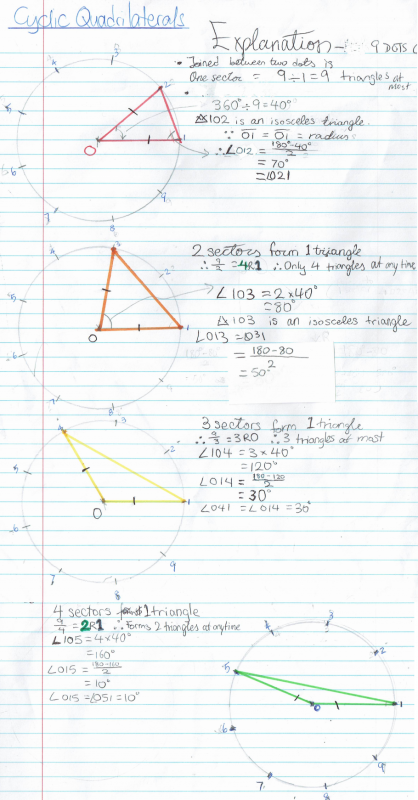
Can you work out the angles of your quadrilaterals?
Freya, Summer, Katie and Phoebe from Long Field Spencer Academy, Ci Hui with images, Shaunak and Thomas and Justin worked out the angles in their quadrilaterals, and/or described a method for doing this. Freya wrote:
I created five quadrilaterals and calculated the angles by dividing them up into triangles. As I have already worked out all the angles in the triangles, I used that information to add up the angles in the quadrilaterals.
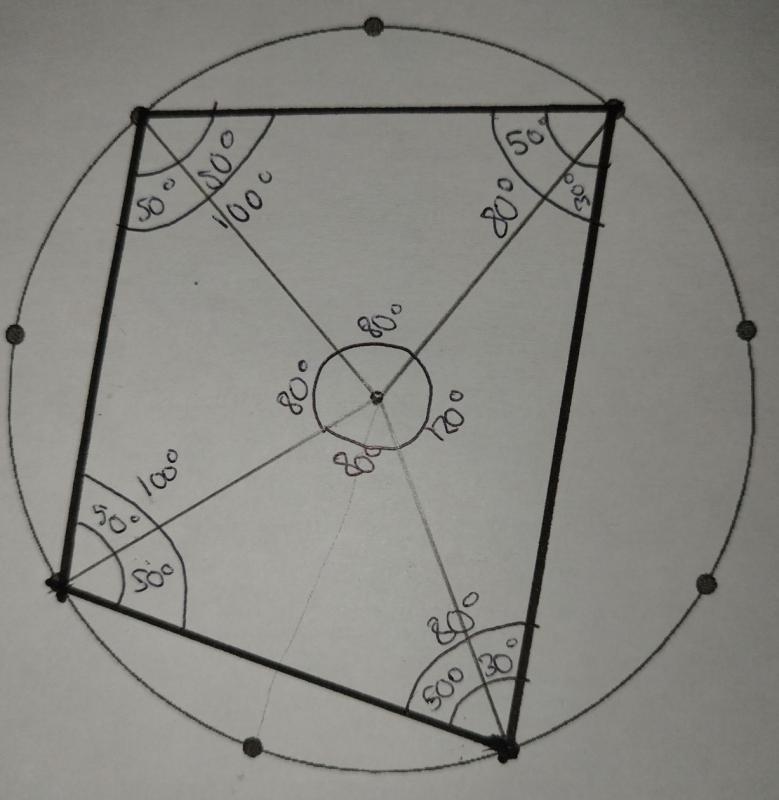
These are some of Katie's quadrilaterals, with the method shown (click on an image to open a larger version):
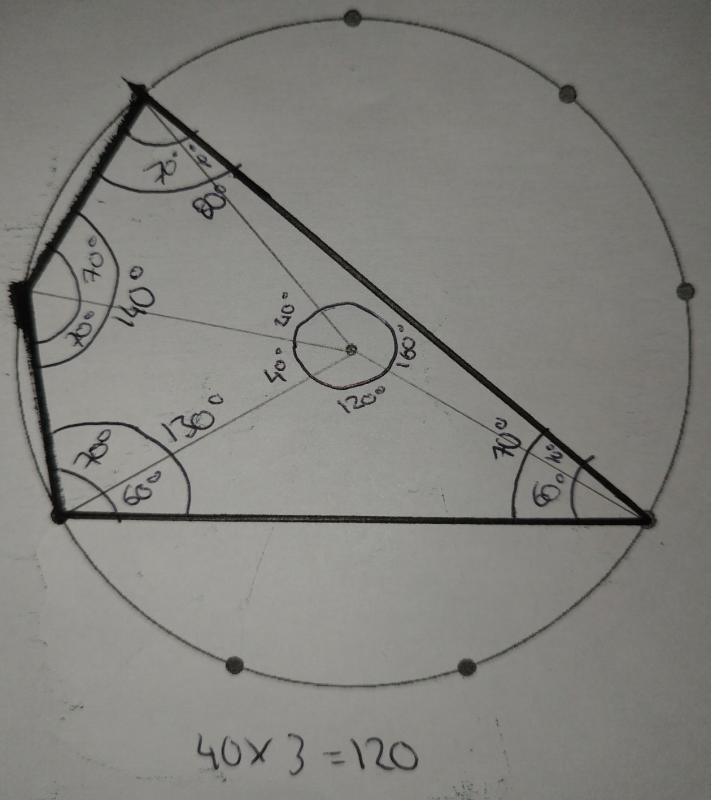
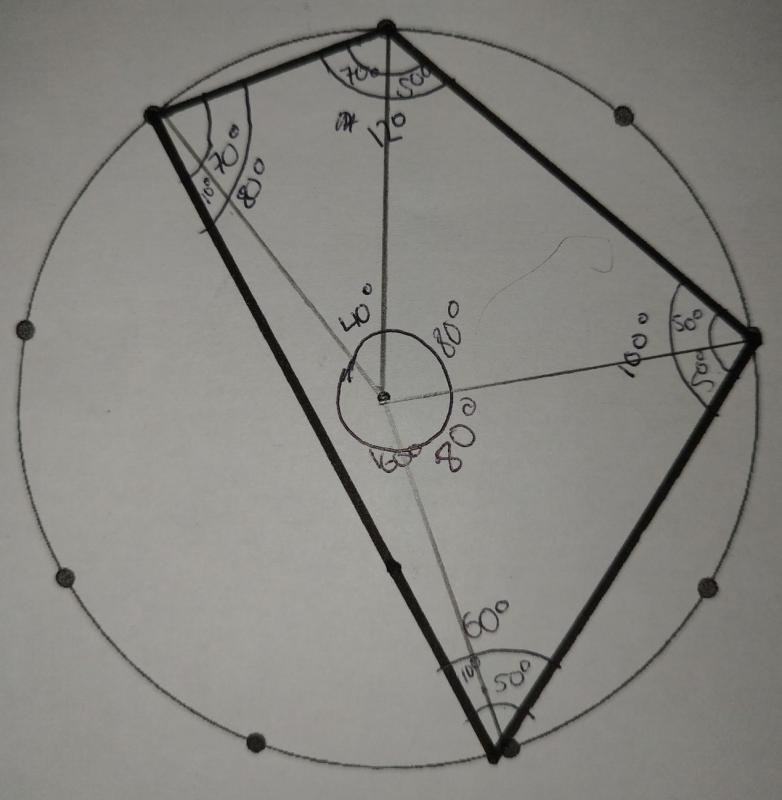
Some of Freya's quadrilaterals were different:
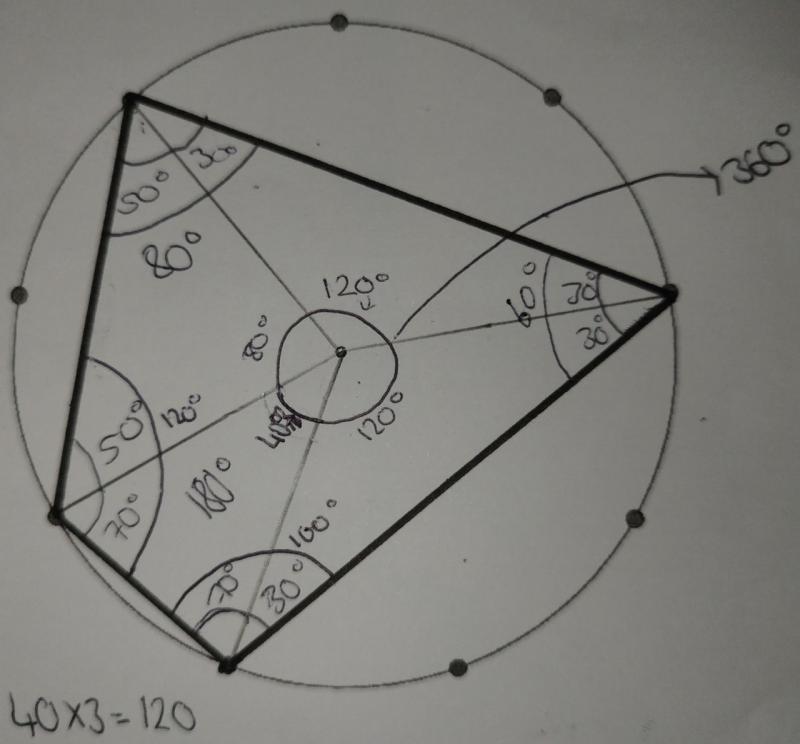
Shaunak had another different quadrilateral:
Finding the angles:
I drew 4 triangles in its inside. This is how it now looked:
I knew the angles of the four triangles. So, I added up the angles in each corner.
In the order of top left, top right, bottom right, bottom left, the angles are 80, 140, 100, 40.
What do you notice about the angles on opposite vertices of your quadrilaterals?
James from Norwich School in the UK, Grace and Ci Hui noticed something about all of the angles. Grace wrote:
All of the angles together would have to add up to 360.
Ci Hui proved this. Click to see Ci Hui's work.
Katie, James, Ci Hui, Shaunak, Thomas and Justin and Freya noticed something about the opposite angles. Katie wrote:
The opposite angles add up to 180 degrees.
You may wish to explore the opposite angles of quadrilaterals on circles with a different number of dots.
Thomas and Justin experimented with other numbers of dots:
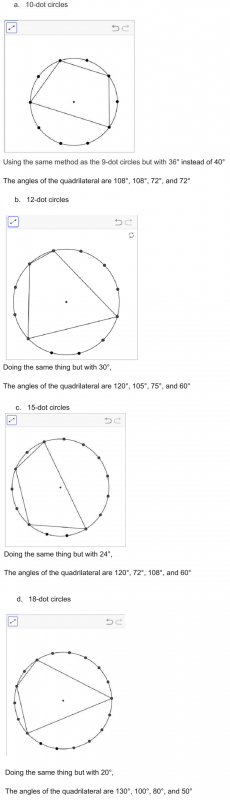
We notice that the sum of the angles on opposite sides of the quadrilaterals is 180 degrees for all of the examples provided above.
Extension:
Will the same happen if you draw a circle and choose four points at random to form a quadrilateral?
Sanaa from Heckmondwike Grammar School in England, James, Katie, Shaunak and Thomas and Justin thought the same thing would happen. Shaunak wrote:
I observed that the sum of opposite angles will be 180.
This must work for any number of dots because even if the number of dots change, the quadrilateral’s properties won’t change.
Sanaa, James and Thomas and Justin proved that the sum of opposite angles in a cyclic quadrilateral is always 180 degrees for cyclic quadrilaterals that contain the centre of the circle. This is Thomas and Justin's proof:
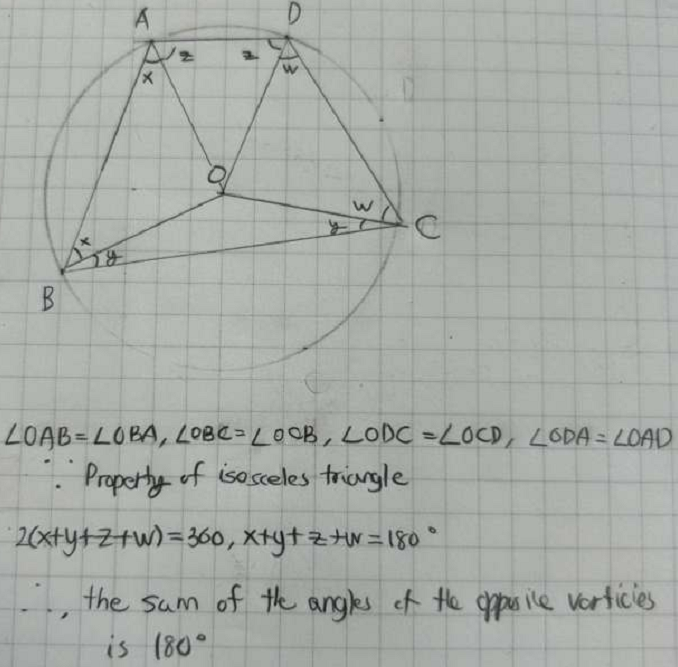
Thomas and Justin and Sanaa also proved that the opposite angles add up to 180 degrees even if the cyclic quadrilateral does not contain the center of the circle. This is Sanaa's proof (click on the image to open a larger version):
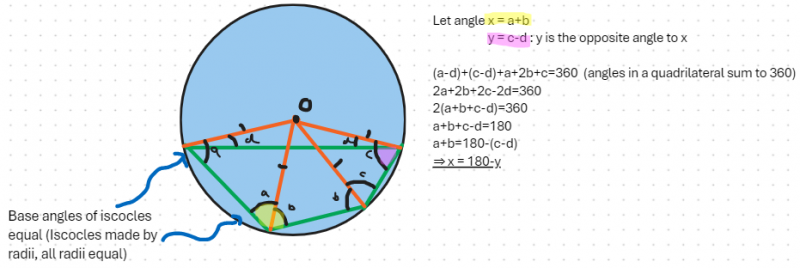
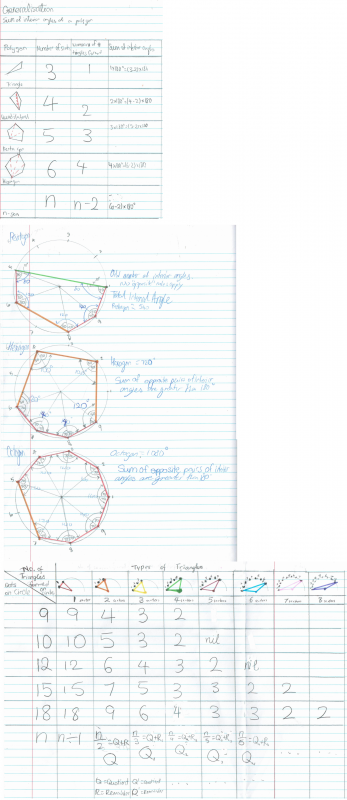
Ci Hui continued the investigation to see what would happen for polygons with other numbers of sides, and circles with other numbers of dots. Click to see the rest of Ci Hui's work.
Click on the image to open a larger version.
Teachers' Resources
Why do this problem?
Possible approach
You can print out 9-point circles with a central dot from our printable resources page for students to work on, or use the GeoGebra applet.
"Draw as many different triangles as you can, by joining the centre dot and any two of the dots on the edge. Can you work out the angles in your triangles, if you know the 9 points are equally spaced around the circle?"
Give students some time to think on their own and then ask them to discuss their ideas with their partners. Then bring the class together and invite students to explain and justify how they calculated each angle.
"We've worked out some angles in triangles, now let's think about quadrilaterals"
"I'd like you to draw some different quadrilaterals by joining four of the nine points around the circle (cyclic quadrilaterals), and then use what you know about angles to work out the angles at the four vertices."
To start with, you may wish students to only draw examples where the centre of the circle lies inside the quadrilateral.
While students are working, you could display an image like the one below to offer a hint for how to work out the angles in the quadrilateral:

Once everyone has had a chance to draw some quadrilaterals and work out the angles, bring the class together and ask a few students to read out the four angles going around one of their quadrilaterals, and draw a table on the board to collect the results. It might look something like this:
| Angle A | Angle B | Angle C | Angle D |
|---|---|---|---|
| 140 | 60 | 40 | 120 |
| 100 | 80 | 80 | 100 |
| 120 | 100 | 60 | 80 |
| 80 | 140 | 100 | 40 |
"Take a look at the table. What do you notice?"
Give students a little thinking time, drawing attention to pairs of columns A and C, and B and D, if no suggestions are forthcoming.
"It looks as though the opposite angles add up to 180 degrees! I wonder if the same would happen if we used circles with more than 9 points?"
This might be a good place to stop, if you're planning to use this task over several lessons.
Hand out 10 dot, 12 dot, 15 dot and 18 dot circles, and invite different groups of students to draw quadrilaterals, work out the angles, and add their results to the table on the board. Once there is a good deal of evidence, bring the class together again.
"Well we haven't found any examples where the opposite angles don't add up to 180 degrees, but that doesn't mean it will always work - I wonder if we can prove it?"
"Will the same happen if you draw a circle and choose four points at random to form a quadrilateral?" - see Possible extension below.
Possible support
Triangles in Circles eases students in a bit more gently to exploring angles on a 9-point circle.
Possible extension
To prove that the opposite angles of all cyclic quadrilaterals add to $180^\circ$ ask students to take a look at Cyclic Quadrilaterals Proof
Students could be challenged to think about cyclic quadrilaterals where the centre of the circle is not contained within the quadrilateral.
Other circle theorems could be explored in a similar way - see Circumference Angles, Subtended Angles and Right Angles.
