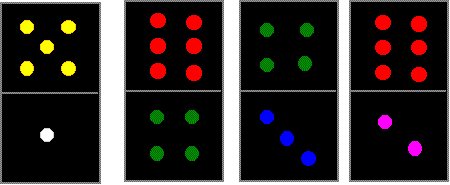
4 dom
Problem
Use these four dominoes to make a square that has the same number of dots on each side.
What did you do to try to solve this challenge?
Here is an interactive you might like to use to try out your ideas.
Click on a domino to rotate it. Use the white x to move a domino around.
Getting Started
And the smallest?
Student Solutions
We had many solutions come in for this task, thank you. We have included some below that also wrote about how they found their answer. All of these found this solution:
Students from Wiripaang Public School in Australia sent in their thoughts and three pictures:
On Wednesday we tried to work out what number the sides of the domino square added up to. We found out it couldn't be 10 or 9 because they were too small. When some of the sides got smaller the other sides got bigger. It couldn't be 14, 15 or 16 because they are too big. When these sides got bigger the others got smaller and it wouldn't work because they weren't even. We thought it might be
11, 12 or 13.
On Thursday we started talking about our superpowers to help us uncover the mystery number. We were working in groups and we decided to use Jakai's superpower to make a plan. We used a number line and started to cross out the numbers it couldn't be. We decided that we couldn't put 6 and 6 together because it made 12 and when we added another number it made it too big. We know that 6 and 4 are
friends often so we would need to put a small number next to it. We started to twist and turn the dominoes until we found that the best number would be 12. Then we keep swapping and twisting until we had 12 on all sides and the sides were even.
Green Maths group from St Joseph's Corinda in Australia wrote:
We started by laying out all the dominoes in the right pattern. We could see that one of the dominoes had dots that added to 10, so the number of dots each side had to be greater than 10.
We then attempted some trial and error (or trial and improvement as we like to call it at NRICH!). Twelve dots on each side quickly became a focus for us, because we could see how easily 12 could be made with the dots given.
By moving the dominoes around in a variety of ways we quickly found our solution.
Brandon from Coten End School wrote
I started out with the domino that has the highest value (6+4=10) at the right side and added a 1 to make a total of 11, which was our target number. The domino with the 1 also had a number of 5 which makes a total of 6, so 11-6=5. But then we realised there was no domino with a 5, so we needed to start again. This time we still used the domino with a total of 10 (6+4=10), but now
added a 2 which made our new total number of 12. The domino with the 2 also had a number of 6, which makes a total of 8. So 12-8=4. There was a domino with a 4 and 3 that makes 7, so 12-7=5. Then I used the remaining domino that had a 5 and 1 to complete the square. This meant the last side had 5+1+6=12. So all sides equal 12.
Nico from Linlithgow Academy in Scotland said:
Because there is a piece with both a six and a four the number of dots in each side must be larger than 10. It also must be smaller than 16.
From there it is possible to use trial and error - or trial and improvement - (with a focus on rotating the dominos rather than moving them every time) to come to the correct answer.
Sam H. from Mabel I. Wilson School in the United States wrote saying:
We knew that the highest sum of three domino sides would be 17. The lowest sum of three sides would be 6. We guessed that the sum of one side of our square would be 10, but we couldn't make it work. We next tried a sum of 12. That sum worked for all four sides!
Teyonne, Amy, Rika from Riverina in New Zealand said:
The smallest number was eight and the biggest number we could make was fourteen. We found we could only make fourteen once and eight twice. So we estimated that it was between nine and thirteen. So we started to lower it down and tested each number.
We also had correct solutions from these pupils:
Daniel from St Peter's Sittingboune; Anaswar from Koodal HSS India; Sandy from Howedell Primary School ; Alesha and Ipshita, Ethan, Ayaan, Ioana and Helena from Huntingdon Primary School; Edmund from Chadwell Primary School; Tania from Avondale Intermediate New Zealand; Chris, Parth, David and
Simar from Gledenning Public School, NSW Australia; Antony from Lockyers Middle School; Zelong from St. John's Beaumont China; Jesse from Channel Christian School Tasmania; Joseph from Hallam Primary School; Tom and Tate from Yanco Public School Australia; Zach, Morgan and Zak from Ravensworth C. of E. Primary
School; Will, Charllie, Alyson and Gurleen from Templeton Primary School Australia; Barn Owl Class from St John's Primary Huntingdon, Rayyan from Doha College Qatar; Cory, Dylan, Zaviour, James from the Riverina School in New Zealand
Well done all of you.
Teachers' Resources
4 Dom
Use these four dominoes to make a square that has the same number of dots on each side.
We would love to see pictures of your completed square but please also tell us what you do to try and solve the challenge.
Here is an interactive you might like to use to try out your ideas.
Click on a domino to rotate it. Use the white x to move a domino around.
Why do this problem?
This problem provides a great opportunity to focus on key problem-solving skills (e.g. trial and improvement) as the level of challenge is provided by there not being an obvious way to solve it, rather than from the number or calculation content. Having said that, however, it does give learners a good reason to develop and use appropriate vocabulary associated with number/calculation. Dominoes are such a versatile resource and having the real thing would be very useful. In this case, the interactivity almost demands more careful planning of where to place a domino compared with use of physical dominoes themselves, and this gives the learner thinking time and space for noticing. 'Noticings' spark children's curiosity, which gives them the motivation to persevere with the task.
Possible approach
One way to engage learners in the task would be to use the interactivity to display four dominoes in a square, but without having equal numbers of dots on all four sides. Invite children to consider what they see and give them time to discuss in pairs before taking contributions within the whole group. Welcome all noticings and once the class has shared their observations, use children's comments to introduce the task itself. You may want to establish the number of dots on each side of your square so that learners have a good understanding of the task.
Ideally, pairs of children will have access to the interactivity on a laptop, computer or tablet, and dominoes, so that they can decide which manipulative they would prefer (or use both). You could print off copies of the printable sheet from the top of the main Problem page to give to pairs. Give them time to begin the task and then draw everyone together for a mini plenary to talk
about how they are getting started. How will they keep track of what they have tried?
Having had more time to work further on the challenge, the plenary could focus on the problem-solving skills they used to solve it. Most children will use trial and improvement and may strike lucky quite quickly. Listen for statements which give an indication that some logical thinking is going on - perhaps in terms of the biggest number a side could add to, or the smallest, or some
acknowledgement of the number of odds and evens which would affect the totals.
Key questions
How many dots are there altogether?
How many dots could there be on each side?
What is the largest total that is possible?
What is the smallest total that is possible?
Possible extension
Children could be asked to create an easier or a harder challenge, similar this one, and to explain what makes their task easier/harder than the original. You could collect the children's own problems and collate them into a book for the rest of the class/school to use.
Possible support
Children who are struggling can be asked to place the dominoes in any position and record the sums for each side. How many different totals can they find?
Which is the biggest? Why?
Which is the smallest? Why?