Circular Inscription
In the diagram, the radius of the circle is equal to the length AB. Can you find the size of angle ACB?
Problem
Image
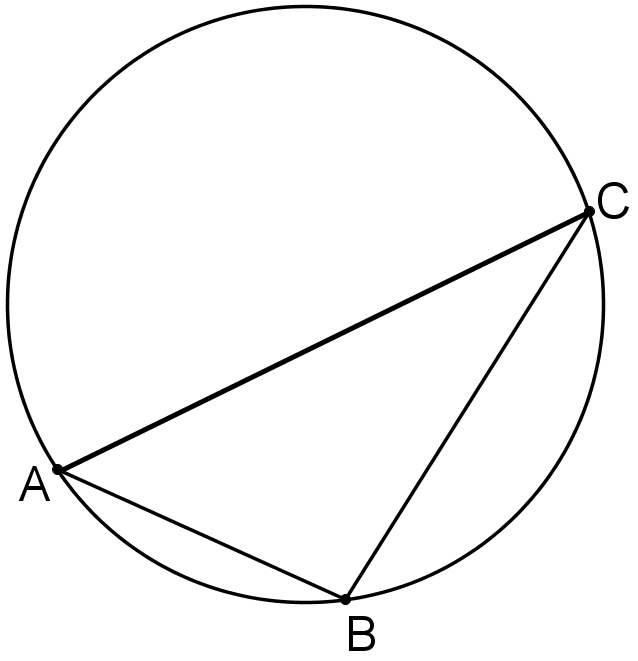
In the diagram, the radius of the circle is equal to the length AB.
What is the size of angle ACB, in degrees?
This problem is taken from the UKMT Mathematical Challenges.
Student Solutions
Using circle theorems
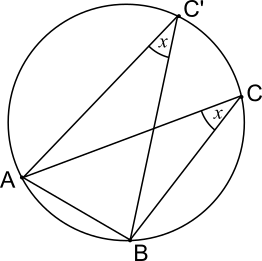
By the circle theorem that angles at the circumference drawn from the same chord are always equal, the point C can be moved around the circumference, such as from C to C' in the diagram below, without changing the angle ACB (marked $x$).
Image
This means that we can choose to put point C diametrically opposite point A, as shown below.
Image
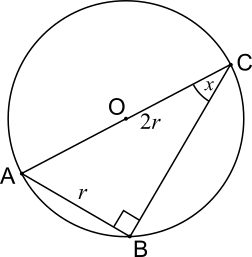
Now, triangle ABC is right-angled because it is a triangle in a semicircle, and since AB is equal to the radius and AC is equal to the diameter, they can be labelled $r$ and $2r$.
Notice that $\triangle OAB$ is equilateral so $\angle OAB=60^{\circ}$ so $\angle ACB=30^{\circ}$.
Or we could use Trigonometry:
$\sin x = \dfrac{\text{opp}}{\text{hyp}}=\dfrac{r}{2r}=\dfrac12$, so $x=30^{\circ}$.
If you are unfamiliar with circle theorems, you can work it out as follows:
Using radii and triangles
In the diagrams below, O is the centre of the circle. The line segments AC, AO, BO and CO have been added. All of the red segments are radii, or AB which is equal to the radius, so they are all equal. Two possible positions for the point C are shown.
Image

Image
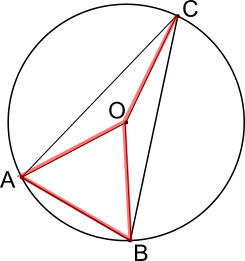
ABO is an equilateral triangle, so all of its angles are 60$^\text o$. ACO and BCO are isosceles, and their equal angles are marked x and y respectively in the diagrams below. In the diagram on the left, CAB is 60$^\text o$- x and ACB is y - x because the line AC divides the angles OAB and OCB.
Image

Image

The sum of the angles in triangle ABC is 180$^\text o$.
Using the triangle on the right, angle ACB is x + y, and x + 60$^\text o$ + 60$^\text o$ + y + y + x = 180$^\text o$.
This simplifies to 2x + 2y + 120$^\text o$ = 180$^\text o$, so 2(x + y) = 60$^\text o$, so x + y = 30$^\text o$.
Using the triangle on the left, angle ACB is y - x, and 60$^\text o$ - x + 60$^\text o$ + y + y - x = 180$^\text o$.
This simplifies to 120$^\text o$ + 2y - 2x = 180$^\text o$, so 2(y - x) = 60$^\text o$, so y - x = 30$^\text o$.
So angle ACB is 30$^\text o$.
