Inspecting identities
Problem
Take a look at these identities.
$$ \cos^2 \frac{\theta}{2} \equiv \frac{1}{2}(1+\cos \theta) \quad \quad \quad \sin^2 \frac{\theta}{2} \equiv \frac{1}{2}(1-\cos \theta)$$
How could you use these identities to help you sketch graphs of $y=\cos^2 \frac{\theta}{2}$ and $y=\sin^2 \frac{\theta}{2}$?
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Student Solutions
Gururvignesh from Hymers College in the UK sent in this solution:
1. We expand $\sin^2\frac x2$ and $\cos^2\frac x2$ so that it equals $\frac12(1-\cos x)$ and $\frac12(1+\cos x)$ respectively
2. We find out the amplitude, period, vertical shift and face shift by substituting the equation $y=a\cos(bx+c)+k$ into the expanded identity.
3. After finding the important points we can sketch the cos or sine graph and label the points.
$y=a\cos(bx+c)+k$
$a$ = amplitude (the height of the graph)
$b$ = period (how long it takes for the graph to repeat)
$c$ = period shift/phase shift
$k$ = vertical shift
$\cos^2\frac x2 = \frac12(1+\cos x)$
$\sin^2\frac x2= \frac12(1-\cos x)$
$\begin{split}y&=\cos^2\tfrac x2\\ &= \frac12+\frac{\cos x}2\end{split}$
$a=\frac12$
period = $\frac{2\pi}b = \frac{2\pi}1=2\pi$
vertical shift = $\frac12$
period shift = $0$
$y = \sin^2\frac x2$
$y =\frac12(1-\cos x)$
$a = -\frac12$ (which means the graph of cosine has to be flipped.)
period = $\frac{2\pi}b = \frac{2\pi}1=2\pi$
vertical shift = $\frac12$
period shift = $0$
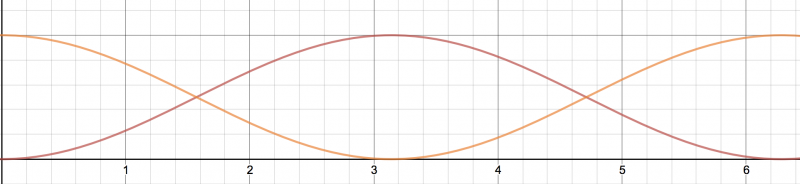
Click here to see a larger image.
The orange graph represents $y= \cos^2 \frac x2$
the red graph represents $y= \sin^2 \frac x2$

