Salt's Mill
A window frame in Salt's Mill consists of two equal semicircles and a circle inside a large semicircle. What is the radius of the circle?
Age
14 to 16
Challenge level
Problem
Image
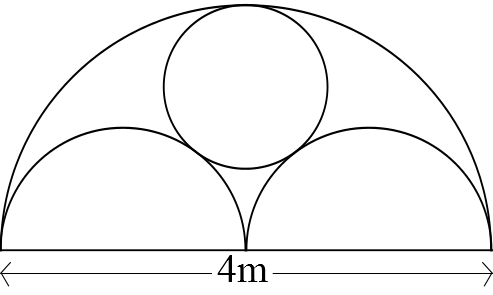
A window frame in Salt's Mill consists of two equal semicircles and a circle inside a large semicircle with each touching the other three as shown. The width of the frame is $4$m.
What is the radius of the circle, in metres?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
What is the radius of the circle, in metres?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Let $A$ be the centre of the circle, $B$ be the centre of the left-hand semicircle and $C$ be the centre of the large semicircle.
Image
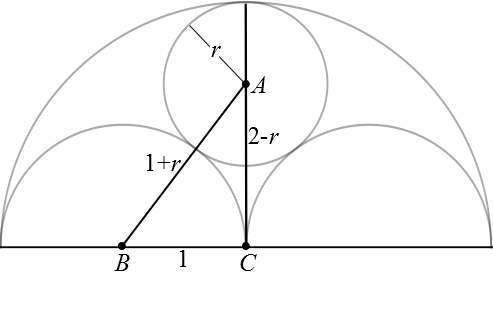
$BC$ has length $1$ because it is a quarter of the diameter of the large semicircle.
$AC$ has length $2-r$ because it is the radius of the large semicircle minus the radius of the circle.
$BA$ has length $1+r$ because it is the sum of the radii of the left-hand semicircle and the circle.
Therefore, by Pythagoras' Theorem:
$$(1+r)^2=1^2+(2-r)^2$$ $$1+2r+r^2=1+4-4r+r^2$$ $$6r=4$$
So the radius is $\frac{2}{3}$ of a metre.