Copyright © University of Cambridge. All rights reserved.
'Probability Through Problems: a new approach to teaching probability' printed from https://nrich.maths.org/
Show menu
This article is part of our collection Great Expectations: Probability through Problems .
.
"Probability is fantastic!"
Perhaps not the usual reaction! But this was the heading of a forum post written by a South African teacher who met our resources recently.
So what's different about our approach:
- we start from a problem, not from a technique
- the progression is from the empirical to the theoretical, with the formal aspects of the curriculum introduced through the problems
- we start each problem with an experiment (using eg. multi-link cubes, specially adapted dice, as well as counters, numbered dice and coins) so that in watching the data accumulate, then analysing it, students can gain a sense of what is happening before being asked to make predictions (which are so often totally ill-informed)
- where dice are used in a model, data is typically collected from 36 trials to make the initial analysis transparent, and so that it is straight-forward to compare what actually happens with what we expect to happen
 data is recorded on a tree diagram and a 2-way table, using natural frequencies (whole numbers)
data is recorded on a tree diagram and a 2-way table, using natural frequencies (whole numbers)- we progress from what happened in the experiment (collating data from all groups in a classroom) to what we would expect to happen
- we then progress from expectation, expressed as a proportion of the number of trials, to probabilities expressed as fractions, using a tree diagram to derive the multiplication rule
All the resources are based on interesting experimental contexts, which model real-life contexts:
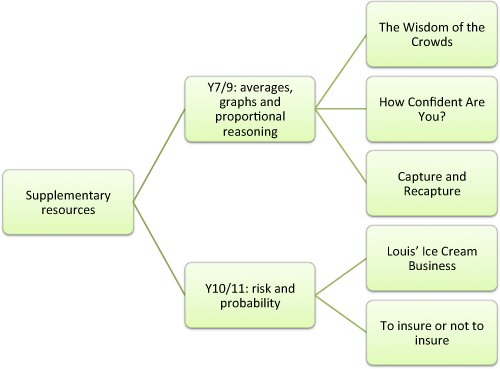
Which team will win? - introducing tree diagrams and the method of collecting data which is then interpreted in terms of what we would expect if we could collect enough data
The dog ate my homework - building on this, expressing expected results in the form of proportions, and hence answering questions about how likely an event is
Who is cheating? - from expected results to probabilities in the form of fractions, and the multiplication rule (and onto conditional probability)
Prize Giving - from experiment to sampling with and without replacement
The dog ate my homework - building on this, expressing expected results in the form of proportions, and hence answering questions about how likely an event is
Who is cheating? - from expected results to probabilities in the form of fractions, and the multiplication rule (and onto conditional probability)
Prize Giving - from experiment to sampling with and without replacement
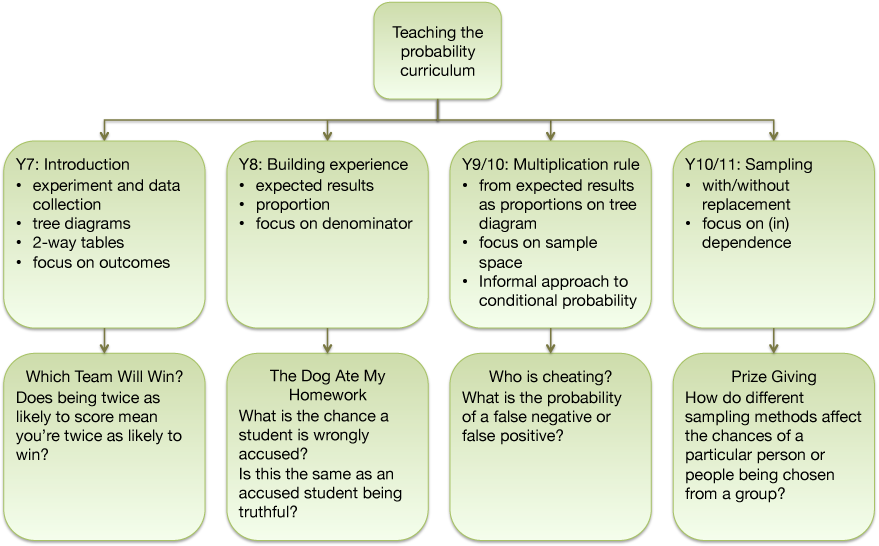
We have a further set of resources which provide additional contexts for exploring the mathematisation of uncertainty and risk:
The Wisdom of the Crowds - exploring averages in the context of skewed data, histograms
How confident are you? - testing people's confidence levels
Capture and re-capture - proportional reasoning through sampling
Louis' Ice Cream Business - what effect does risk have on assessment of likely outcomes
To insure or not to insure - risk from the perspective of the owner of a mobile phone and a company that wants to make money out of insurance
How confident are you? - testing people's confidence levels
Capture and re-capture - proportional reasoning through sampling
Louis' Ice Cream Business - what effect does risk have on assessment of likely outcomes
To insure or not to insure - risk from the perspective of the owner of a mobile phone and a company that wants to make money out of insurance