Christmas Boxes
Problem
Find all the ways to cut out a 'net' of six squares that can be folded into a cube. Here's two to get you started.



Getting Started
It may help to work on squared paper.
Student Solutions
There were 11 possibilites in total, found by George and Jannis. Well Done for cracking ths Toughnut!
George (Rosebank Primary School, Leeds) recognised this type of problem. He described his answers in groups as well as drawing them, finding 7 of the possibilities.
"We did this sum at school last year and this is what I think the answer is. First I did this kind of boxes. They were 4 squares down, 1 square at the top left and one at the bottom right. I looked for more and I found that there was only 1:

Then I did this kind of boxes. They were 4 squares down, then one square
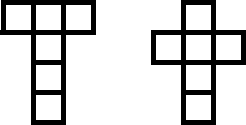
at the left and opposite it the right one. There were 2 of these:
After that I did this kind of boxes. They were 4 squares down, 1 square at the left and then a right square which will be opposite then 1 square up or down. There were 2 of these:
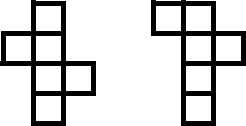
Fourthly I did this kind of boxes. They were 4 squares down, 1 square at the left and a right one which will be opposite then 2 squares up or down. There was only 1 of them: At last I did this kind of boxes. They were 3 squares down and 3 squares which the last of their square is touching the last of the 1st 3 squares. There was only one of them:
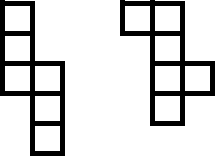
The answer is you can make 7 boxes".
Jannis (Long Bay Primary) then correctly found the other 4:
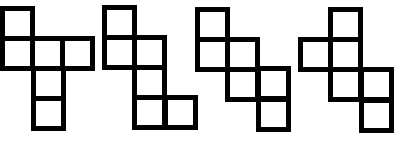
Finally, Matthew (Eastwood Primary) noticed that:
"You can turn them around or reflect them to make a lot more."So there are other possibilites, but they would just be rotations or reflections of the above 11.
Teachers' Resources
Teachers may want to provide students with squared paper for this problem.
One way of introducing this problem is to challenge students to first find all the different ways of arranging two squares (dominoes), three squares (triominoes), four squares (tetrominoes), five squares (pentominoes) and six squares (hexominoes) - all the squares must touch at least one other square along one of its edges (with the edges lining up exactly).
| Number of Squares | Number of Arrangements |
| 2 | 1 |
| 3 | 2 |
| 4 | 5 |
| 5 | 12 |
| 6 | 35 |
