Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
A Circuit Problem
Age 16 to 18
ShortChallenge Level 





- Problem
- Getting Started
- Solutions
Starting at the right hand side of the circuit, assume a current of 1A flows in resistor X, and work out the potential drops back to the voltage source. Then use scaling.
Let $I_x$ = 1 amp and find the corresponding V.
We can then use scaling to find $I_x$ when V = 14V.
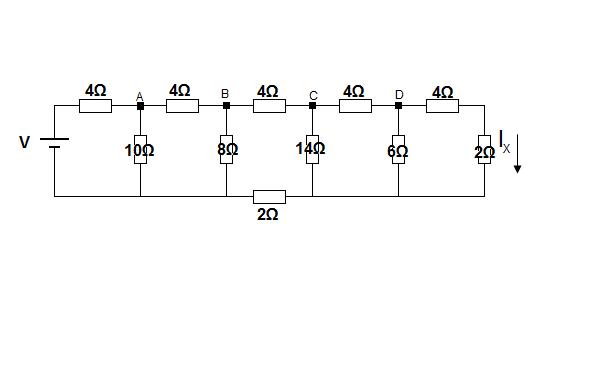
Working right to left:
$I_x$= 1
Find the voltage at d
$V_d = I_x ( 4 + 2) $ = 6V
Find the voltage at c
$V_c = V_d + V_{cd} = V_d + 4I_{cd}$ (Kirchoff's voltage law)
$I_{cd} = I_{d} + I_{x}$ = $\frac{V_d}{6} + 1 = 2$ (Kirchoff's current law)
$V_c = 6V + 8V = 14V $
Find the voltage at b
$V_b= V_c + V_{bc} + (I_x + I_d + I_c)2 $
$I_x = 1$
$I_d = \frac{V_d}{6} = 1$
$I_c = \frac{V_c}{14} = 1$
$I_{bc} = I_c + I_{cd} = 3$(Kirchoff's current law)
$V_b = V_c + 4I_{bc} + 6 $ = $ 14 + 12 + 6 = 32V $(Kirchoff's voltage law)
Find the voltage at a
$V_a = V_b + V_{ab} = V_b + 4I_{ab}$
$I_{ab} = I_{bc} + I_b = 3 + \frac{32}{8} = 7$
$V_a = 32 + 28 = 6OV$
Find V when $I_x = 1$
V = $V_a + 4I_{0a}$
$I_{0a} = I_{ab} + \frac{V_a}{10} = 13A$
$V = 60 + 52 = 112V$
We know that in reality V = 14V
All loads are completely resistive, the relationship between voltage and current is therefore linear.
The current which would have given a voltage of 14 V is therefore 1 x $\frac{14}{112}$= 0.125 A
$I_x$ = 0.125 A

