Copyright © University of Cambridge. All rights reserved.
'What Numbers Can We Make?' printed from https://nrich.maths.org/
Show menu
Lots of people added together three numbers and noticed something special! For example, Emma, from Interlakes Elementary, told us her findings:
I figured out that, if you kept adding the numbers together, they will always come to a multiple of 3 every time you do it.
Charlie, from St. Cecilia's Wandsworth, noticed:
What we did was: we started with 3 numbers, then we added them together, and we noticed that some were odd and some were even but they were all multiples of 3. Then we tried adding 4 numbers, and we found that the answers were 1 more than the numbers in the 3 times table. Choosing 5 numbers we got answers which were 2 more than the 3 times table. We guessed that adding 6 numbers would give answers back in the 3 times table.
Great observations! Bethan, Gareth and Aditya, from St. Nicolas CE Junior School, offered an explanation of this. Bethan wrote:
When you have your three numbers, say 4, 7 and 1, each of these numbers is 1 more than a multiple of 3.
So 3+1, 6+1 and 0+1.
Then when you add them together, you can add the 3, 6 and 0 together which makes a multiple of 3, plus the three 1s left over will add together to also make a multiple of 3.
This makes your overall answer a multiple of 3.
Good! (Is this related to either Charlie's or Alison's method?) Aditya used the same method to notice:
Adding together 99 numbers would give a multiple of 3, and 100 numbers would equal a multiple of 3 plus 1.
Brandyn from Garden International School considered what happened when he added sets of 3, 4, 5, 6 and 99 numbers from the bags below:
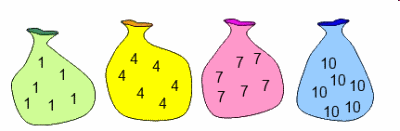
Choosing four numbers from the bags above gave the following totals, all 1 more than (or 2 less than) multiples of 3:
Excellent. Thanks!
I figured out that, if you kept adding the numbers together, they will always come to a multiple of 3 every time you do it.
Charlie, from St. Cecilia's Wandsworth, noticed:
What we did was: we started with 3 numbers, then we added them together, and we noticed that some were odd and some were even but they were all multiples of 3. Then we tried adding 4 numbers, and we found that the answers were 1 more than the numbers in the 3 times table. Choosing 5 numbers we got answers which were 2 more than the 3 times table. We guessed that adding 6 numbers would give answers back in the 3 times table.
Great observations! Bethan, Gareth and Aditya, from St. Nicolas CE Junior School, offered an explanation of this. Bethan wrote:
When you have your three numbers, say 4, 7 and 1, each of these numbers is 1 more than a multiple of 3.
So 3+1, 6+1 and 0+1.
Then when you add them together, you can add the 3, 6 and 0 together which makes a multiple of 3, plus the three 1s left over will add together to also make a multiple of 3.
This makes your overall answer a multiple of 3.
Good! (Is this related to either Charlie's or Alison's method?) Aditya used the same method to notice:
Adding together 99 numbers would give a multiple of 3, and 100 numbers would equal a multiple of 3 plus 1.
Brandyn from Garden International School considered what happened when he added sets of 3, 4, 5, 6 and 99 numbers from the bags below:
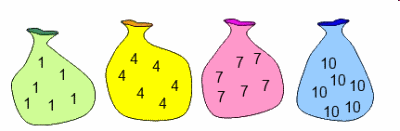
Choosing just three numbers from the bags above gave the following totals, all multiples of 3:
| 1 | 4 | 7 | 10 | TOTAL |
| 3 | 3 | |||
| 3 | 12 | |||
| 3 | 21 | |||
| 3 | 30 | |||
| 2 | 1 | 6 | ||
| 2 | 1 | 9 | ||
| 2 | 1 | 12 | ||
| 1 | 2 | 9 | ||
| 2 | 1 | 15 | ||
| 2 | 1 | 18 | ||
| 1 | 2 | 15 | ||
| 1 | 2 | 18 | ||
| 2 | 1 | 24 | ||
| 1 | 2 | 21 | ||
| 1 | 2 | 24 | ||
| 1 | 2 | 27 | ||
| 1 | 1 | 1 | 12 | |
| 1 | 1 | 1 | 15 | |
| 1 | 1 | 1 | 18 | |
| 1 | 1 | 1 | 21 |
Choosing four numbers from the bags above gave the following totals, all 1 more than (or 2 less than) multiples of 3:
| 1 | 4 | 7 | 10 | TOTAL |
| 4 | 4 | |||
| 4 | 16 | |||
| 4 | 28 | |||
| 4 | 40 | |||
| 3 | 1 | 7 | ||
| 3 | 1 | 10 | ||
| 3 | 1 | 13 | ||
| 1 | 3 | 13 | ||
| 3 | 1 | 19 | ||
| 3 | 1 | 22 | ||
| 1 | 3 | 22 | ||
| 1 | 3 | 25 | ||
| 3 | 1 | 31 | ||
| 1 | 3 | 31 | ||
| 1 | 3 | 34 | ||
| 1 | 3 | 37 | ||
| 2 | 2 | 10 | ||
| 2 | 2 | 16 | ||
| 2 | 2 | 22 | ||
| 2 | 2 | 22 | ||
| 2 | 2 | 28 | ||
| 2 | 2 | 34 | ||
| 2 | 1 | 1 | 13 | |
| 2 | 1 | 1 | 16 | |
| 2 | 1 | 1 | 19 | |
| 1 | 2 | 1 | 16 | |
| 1 | 2 | 1 | 19 | |
| 2 | 1 | 1 | 25 | |
| 1 | 1 | 2 | 19 | |
| 1 | 2 | 1 | 25 | |
| 1 | 2 | 1 | 28 | |
| 1 | 1 | 2 | 25 | |
| 1 | 1 | 2 | 28 | |
| 1 | 1 | 2 | 31 | |
| 1 | 1 | 1 | 1 | 22 |
If I choose 5 numbers I predict that the series will start with 5 and increase in 3's.
If I choose 6 numbers I predict that the series will start with 6 and increase in 3's, etc..
If I choose 99 numbers, I predict that the series will start with 99 and increase in 3's.
Excellent. Thanks!