Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
What Numbers Can We Make?
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Lots of people added together three numbers and noticed something special! For example, Emma, from Interlakes Elementary, told us her findings:
I figured out that, if you kept adding the numbers together, they will always come to a multiple of 3 every time you do it.
Charlie, from St. Cecilia's Wandsworth, noticed:
What we did was: we started with 3 numbers, then we added them together, and we noticed that some were odd and some were even but they were all multiples of 3. Then we tried adding 4 numbers, and we found that the answers were 1 more than the numbers in the 3 times table. Choosing 5 numbers we got answers which were 2 more than the 3 times table. We guessed that adding 6 numbers would give answers back in the 3 times table.
Great observations! Bethan, Gareth and Aditya, from St. Nicolas CE Junior School, offered an explanation of this. Bethan wrote:
When you have your three numbers, say 4, 7 and 1, each of these numbers is 1 more than a multiple of 3.
So 3+1, 6+1 and 0+1.
Then when you add them together, you can add the 3, 6 and 0 together which makes a multiple of 3, plus the three 1s left over will add together to also make a multiple of 3.
This makes your overall answer a multiple of 3.
Good! (Is this related to either Charlie's or Alison's method?) Aditya used the same method to notice:
Adding together 99 numbers would give a multiple of 3, and 100 numbers would equal a multiple of 3 plus 1.
Brandyn from Garden International School considered what happened when he added sets of 3, 4, 5, 6 and 99 numbers from the bags below:
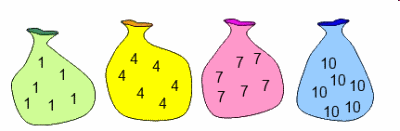
Choosing four numbers from the bags above gave the following totals, all 1 more than (or 2 less than) multiples of 3:
Excellent. Thanks!
I figured out that, if you kept adding the numbers together, they will always come to a multiple of 3 every time you do it.
Charlie, from St. Cecilia's Wandsworth, noticed:
What we did was: we started with 3 numbers, then we added them together, and we noticed that some were odd and some were even but they were all multiples of 3. Then we tried adding 4 numbers, and we found that the answers were 1 more than the numbers in the 3 times table. Choosing 5 numbers we got answers which were 2 more than the 3 times table. We guessed that adding 6 numbers would give answers back in the 3 times table.
Great observations! Bethan, Gareth and Aditya, from St. Nicolas CE Junior School, offered an explanation of this. Bethan wrote:
When you have your three numbers, say 4, 7 and 1, each of these numbers is 1 more than a multiple of 3.
So 3+1, 6+1 and 0+1.
Then when you add them together, you can add the 3, 6 and 0 together which makes a multiple of 3, plus the three 1s left over will add together to also make a multiple of 3.
This makes your overall answer a multiple of 3.
Good! (Is this related to either Charlie's or Alison's method?) Aditya used the same method to notice:
Adding together 99 numbers would give a multiple of 3, and 100 numbers would equal a multiple of 3 plus 1.
Brandyn from Garden International School considered what happened when he added sets of 3, 4, 5, 6 and 99 numbers from the bags below:
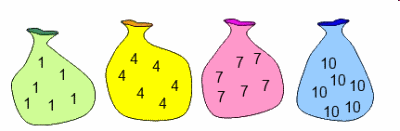
Choosing just three numbers from the bags above gave the following totals, all multiples of 3:
| 1 | 4 | 7 | 10 | TOTAL |
| 3 | 3 | |||
| 3 | 12 | |||
| 3 | 21 | |||
| 3 | 30 | |||
| 2 | 1 | 6 | ||
| 2 | 1 | 9 | ||
| 2 | 1 | 12 | ||
| 1 | 2 | 9 | ||
| 2 | 1 | 15 | ||
| 2 | 1 | 18 | ||
| 1 | 2 | 15 | ||
| 1 | 2 | 18 | ||
| 2 | 1 | 24 | ||
| 1 | 2 | 21 | ||
| 1 | 2 | 24 | ||
| 1 | 2 | 27 | ||
| 1 | 1 | 1 | 12 | |
| 1 | 1 | 1 | 15 | |
| 1 | 1 | 1 | 18 | |
| 1 | 1 | 1 | 21 |
Choosing four numbers from the bags above gave the following totals, all 1 more than (or 2 less than) multiples of 3:
| 1 | 4 | 7 | 10 | TOTAL |
| 4 | 4 | |||
| 4 | 16 | |||
| 4 | 28 | |||
| 4 | 40 | |||
| 3 | 1 | 7 | ||
| 3 | 1 | 10 | ||
| 3 | 1 | 13 | ||
| 1 | 3 | 13 | ||
| 3 | 1 | 19 | ||
| 3 | 1 | 22 | ||
| 1 | 3 | 22 | ||
| 1 | 3 | 25 | ||
| 3 | 1 | 31 | ||
| 1 | 3 | 31 | ||
| 1 | 3 | 34 | ||
| 1 | 3 | 37 | ||
| 2 | 2 | 10 | ||
| 2 | 2 | 16 | ||
| 2 | 2 | 22 | ||
| 2 | 2 | 22 | ||
| 2 | 2 | 28 | ||
| 2 | 2 | 34 | ||
| 2 | 1 | 1 | 13 | |
| 2 | 1 | 1 | 16 | |
| 2 | 1 | 1 | 19 | |
| 1 | 2 | 1 | 16 | |
| 1 | 2 | 1 | 19 | |
| 2 | 1 | 1 | 25 | |
| 1 | 1 | 2 | 19 | |
| 1 | 2 | 1 | 25 | |
| 1 | 2 | 1 | 28 | |
| 1 | 1 | 2 | 25 | |
| 1 | 1 | 2 | 28 | |
| 1 | 1 | 2 | 31 | |
| 1 | 1 | 1 | 1 | 22 |
If I choose 5 numbers I predict that the series will start with 5 and increase in 3's.
If I choose 6 numbers I predict that the series will start with 6 and increase in 3's, etc..
If I choose 99 numbers, I predict that the series will start with 99 and increase in 3's.
Excellent. Thanks!