Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cyclic Quad Jigsaw
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions
- Teachers' Resources
We had two very clear solutions to this problem - well done to James, from Poole Grammar School, and Dylan, who did not give his school. James's solution is shown here.
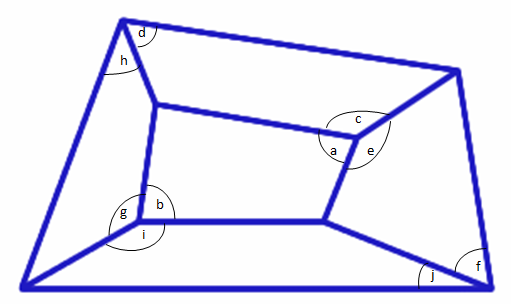
All five of the small quadrilaterals in the above shape are
cyclic, and by using the fact that opposite angles in a cyclic
quadrilateral add up to $180 ^{\circ}$ we can prove that the large
quadrilateral made up of the five smaller ones is also
cyclic.
Opposite angles in each cyclic quadrilateral add up to
$180^{\circ}$, so we can write expressions for angles $a$, $c$, and
$e$.
$$a = 180^{\circ}- b$$ $$c = 180^{\circ}- d$$ $$e =
180^{\circ}- f$$
Angles $a$, $c$, and $e$ are all round the same point
therefore: $$360^{\circ} = a + c + e$$ Substituting in the
expressions for angles c and e in we get: $$360^{\circ} = a +
(180^{\circ} - d) + (180^{\circ} - f)$$
Simplifying this we get: $$360^{\circ} = a + 360^{\circ} - d -
f$$ $$ a = d + f$$
Now we follow exactly the same working with the other side of
the quadrilateral which gives us the equation $$b = h + j$$
We also know that $a + b = 180^{\circ}$ because they are
opposite angles in a cyclic quadrilateral. Substituting in the
expressions for $a$ and $b$ gives us $$d + f + h + j =
180^{\circ}$$
So $$(d + h) = 180^{\circ} - (f + j)$$
Looking back at the original diagram we can see that $(d + h)$
and $(f +j)$ are opposite angles in the quadrilateral and because
$(d + h) = 180^{\circ} - (f + j)$ the quadrilateral must be
cyclic.