Stage: 4 Challenge Level: 
Someone showed me this picture of a quadrilateral made by joining together five smaller quadrilaterals.
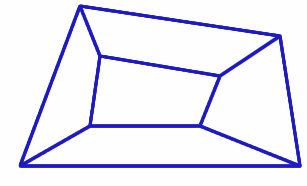
It made me think about special cases...
Could I draw a version of this image where all five of the
smaller quadrilaterals are cyclic? I tried it out and have
tried to capture what I did, and what the question was that it
made me want to answer, in the video below:
This text is usually replaced by the Flash movie.
Can you convince us that the largest quadrilateral is also
cyclic?
Circle theorems. Mathematical reasoning & proof. Inequality/inequalities. Patterned numbers. Visualising. Manipulating algebraic expressions/formulae. Generalising. Number theory. Dynamical systems. Quadrilaterals.
Published June 2000,March 2009,April 2009.
Copyright © 2007. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project, which also includes the Plus and Motivate sites.
email: nrich@damtp.cam.ac.uk
