Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Robert's Spreadsheet
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Adithya from Lexden Primary School noted that there is a pattern to the gap between square numbers, with the gap increasing by two each time. Adithya also noticed a pattern in column A; this was also spotted by James from Wilson's School, Niteesh from Vidyashilp Academy, Dan and Linden from Wilson's School, and James from Eltham College. Here is a picture of Linden's spreadsheet showing the pattern:
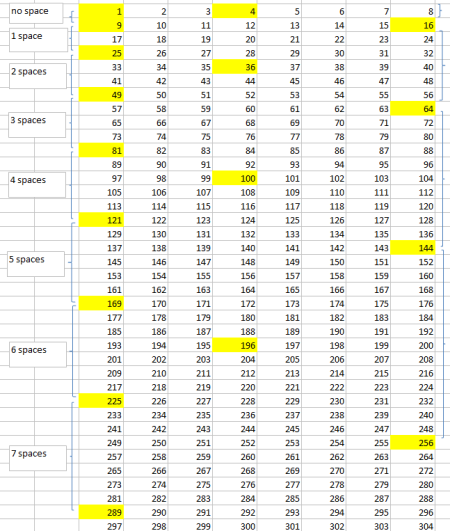
Krystof from Uhelny Trh, Prague, made some comments about which squares appear in each column:
Column A contains squares of odd numbers. Column D contains squares of even numbers which are not divisible by four. Column H contains squares of multiples of four.
An anonymous solver sent us these thoughts:
Firstly I noticed that all of the squares of odd numbers were in the left-hand column, column A. All of the squares of even multiples of 4 were in the right-hand column, column H, while all of the squares of other even numbers are in column D.
I can explain these by saying that the squares of multiples of $4$ are always multiples of $8$. The squares of any other even numbers are always multiples of $4$, while the squares of odd numbers do not all have a common factor and therfore are only divisble by one.
I noticed that the final digit of the odd squares was always $1$, $5$ or $9$ and for the even squares always $4$, $6$ or $0$. I also noticed that the first square number was in column A, then the second in column D, the third back in column A and the fourth in column H. I also noticed that in column A, which has the squares of odd numbers, the rows between the squares increases by $1$ every time, for example there are $0$ rows between $1$ and $9$, $1$ row between $9$ and $25$, $2$ rows between $25$ and $49$ etcetera. This therefore tells me that the difference between odd numbers is also always a multiple of $8$.
I can also see that when each odd square is represented in the form $2n+1$ $n$ is always a multiple of $4$ ($2\times4+1=9, 2\times40+1=81$ etc.) I can use examples to demonstrate this, for example $13\times13=169$ which not only ends in $9$ but is also $2\times84+1$, and $84$ is a multiple of $4$. Not only this, the difference between $169$ and the previous odd square is $48$, which is a multiple of $8$, just like the pattern suggested. The patterns also work for the next square numbers, i.e. $14\times14=196$ and $15\times15=225$.
Lots of fantastic ideas - can it be proved that these patterns will continue?
Herschel from the European School of Varese, and Simon who didn't give his school both sent us algebraic explanations for some of the patterns. Here is Herschel's solution:
The square numbers show a definite pattern:
$1^2=1$ is in column A.
$2^2=4$ is in column D.
$3^2=9$ is in column A.
$4^2=16$ is in column H.
This pattern (A,D,A,H) repeats itself throughout the series, albeit with larger gaps (blank rows) as the numbers increase.
This can be proven algebraically:
Suppose we call $n$ any multiple of $4$ We can write any whole number as either $n$, $n+1$, $n+2$ or $n+3$. Since $n$ is a multiple of $4$, we can re-write $n$ as $4a$, so that all whole numbers are either $4a$, $4a+1$, $4a+2$ or $4a+3$.
$(4a)^2 = 16a^2$, which is $8\times(2a^2)$, so it is a multiple of $8$ and hence appears in column H.
$(4a+1)^2 = 16a^2+8a+1$ which is $8\times(2a^2+a) + 1$, so it is $1$ more than a multiple of $8$ and hence appears in column A.
$(4a+2)^2 = 16a^2+16a+4$ which is $8\times(2a^2+2a) + 4$, so it is $4$ more than a multiple of $8$ and hence appears in column D.
$(4a+3)^2 = 16a^2+24a+9$ which is $8\times(2a^2+3a+1) + 1$, so it is $1$ more than a multiple of $8$ and hence appears in column A.
After $4a+3$, the next number is $4a+4$ which is $4(a+1)$, so we increase $a$ by $1$ and continue the trend. This means the pattern of highlighted squares is H,A,D,A (or A,D,A,H since we ignore $0^2=0$) and this continues forever.
Well done to all those who submitted solutions!