Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Robert's Spreadsheet
Age 14 to 16
Challenge Level 





Robert made a spreadsheet with eight columns. He arranged the numbers from 1 to 1000 in his spreadsheet, and then coloured in all the square numbers.
Here is a picture showing the first few rows of Robert's spreadsheet:
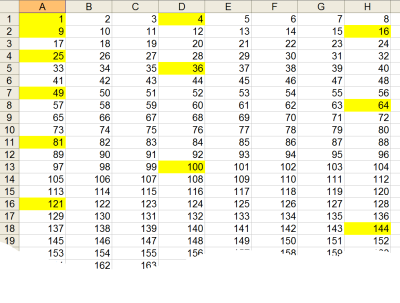
Robert noticed some interesting patterns beginning to emerge.
Why not create your own copy of Robert's spreadsheet and see what patterns you notice?
Can you explain the patterns you find?
Will the patterns continue? How can you be sure?