Napkin

This solution is a combination of the work of David from Trinity School and several others.

A square is folded so that the corner $E$ coincides with the midpoint of an opposite edge as shown in the diagram. The length of the edge of the square is 1 unit and the problem is to find the lengths and areas of the three triangles.

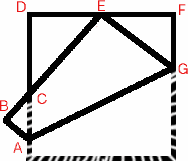
The table shows the solutions:

Triangle	Lengths of sides 3 : 4 : 5	Ratio of lengths in 3 triangles	Area	Ratio of areas of 3 triangles
EGF	3/8 : 1/2 : 5/8	3	3/32	9
CED	1/2 : 2/3 : 5/6	4	1/6	16
CAB	1/8 : 1/6 : 5/24	1	1/96	1

This is David's method:

The edge, $EF = 1/2$. Taking $FG = a$ then $GE = 1-a$

As it has a corner of the paper as part of it, we know $EGF$ is a right angled triangle, and so $GE^2 = EF^2 + FG^2$, which gives \[ (1-a)^2 = 1/4 + a^2 \]

so \[a = 3/8.\]

Now that we have the length of $a$, we have the lengths of all the sides of this triangle: $EF = 1/2$ , $FG = 3/8$ and $GE = 5/8.$

At this point, David uses Trigonometry to complete the problem, but other solutions just used similar triangles.

The area of triangle $EFG = 1/2$ base $\times$ height $ = 3/32$.

Using this information and trigonometry, we can work out the angle $GEF$: $\angle GEF = \tan^{-1}(0.375 / 0.5) = \tan^{-1}0.75 = 36.9^{\circ}.$

taking the angle to the nearest tenth of a degree. Knowing this, we can work out the angle $DEC=53.1^{\circ}$ and use it with the length $DE$ to work out the length $DC=2/3.$ The last part needed of this triangle is $CE$ and, using Pythagoras' theorem, we get $CE =5/6.$

So $DE = {1 \over 2}$, $DC = {2 \over 3}$, $CE = {5 \over 6}$ and the area of triangle $DEC = 1/2 \times 2/3 \times 1/2 = {1 \over 6}.$

The last triangle needed is $ABC$. We know the length $BC = 1 - CE = 1/6.$ We can also work out the angle $BCA $ which is equal to angle $DCE$ and to angle $FEG.$ We can now use trigonometry to work out the length $AB = 1/6 \tan BCA = 1/8.$

And so once again, using Pythagoras, we can work out the length of line $AC$ which is $5/24.$

And so we have the final set of lengths: $AB = 1/8$, $BC = 1/ 6$ and $AC = 5/24.$

The area of triangle $ABC = 1/2 \times 1/8 \times 1/6 = 1/96$.

This means the total area of all the paper with a single thickness = $26/96 = .270833..$

This can be backed up by working out the area of the trapezium $ABEG$, subtracting the area of triangle $ABC$ and then multiplying the result by 2 to give the area of the original square that is now double thickness.

Area of trapezium = $1/2 [1/8 +5/8] \times 1 = 3/8.$ Double thickness area = $3/8 - 1/96 = 35/96.$

The total area is $2 \times 35/96 + 26/96= 1$ and so all areas are worked out and recorded, and the total area of single thickness paper and double thickness areas are recorded.

Triangle EFG has sides in the ratio $3:4:5$, so triangle CDE must also have sides in the ratio $3:4:5$.

$CD = {1 \over 2} \div 3 \times 4$

$CD = {2 \over 3}$

$CE = {1 \over 2} \div 4 \times 5$

$CE = {5 \over 8}$

$EB$ is a side of the square, so $EB$ is 1 unit.
$BC = 1- {5 \over 6}$
$BC = {1 \over 6}$

$BC$ is the $4$ side of the 3:4:5 triangle.

$BA = {1 \over 6} \div 4 \times 3$

$BA = {3 \over {24}}$

$AC = {1 \over 6} \div 4 \times 5$

$AC = {5 \over {24}}$