This problem follows on from Clock Arithmetic and More Adventures with Modular Arithmetic.

Start by considering square numbers in modulo $5$.

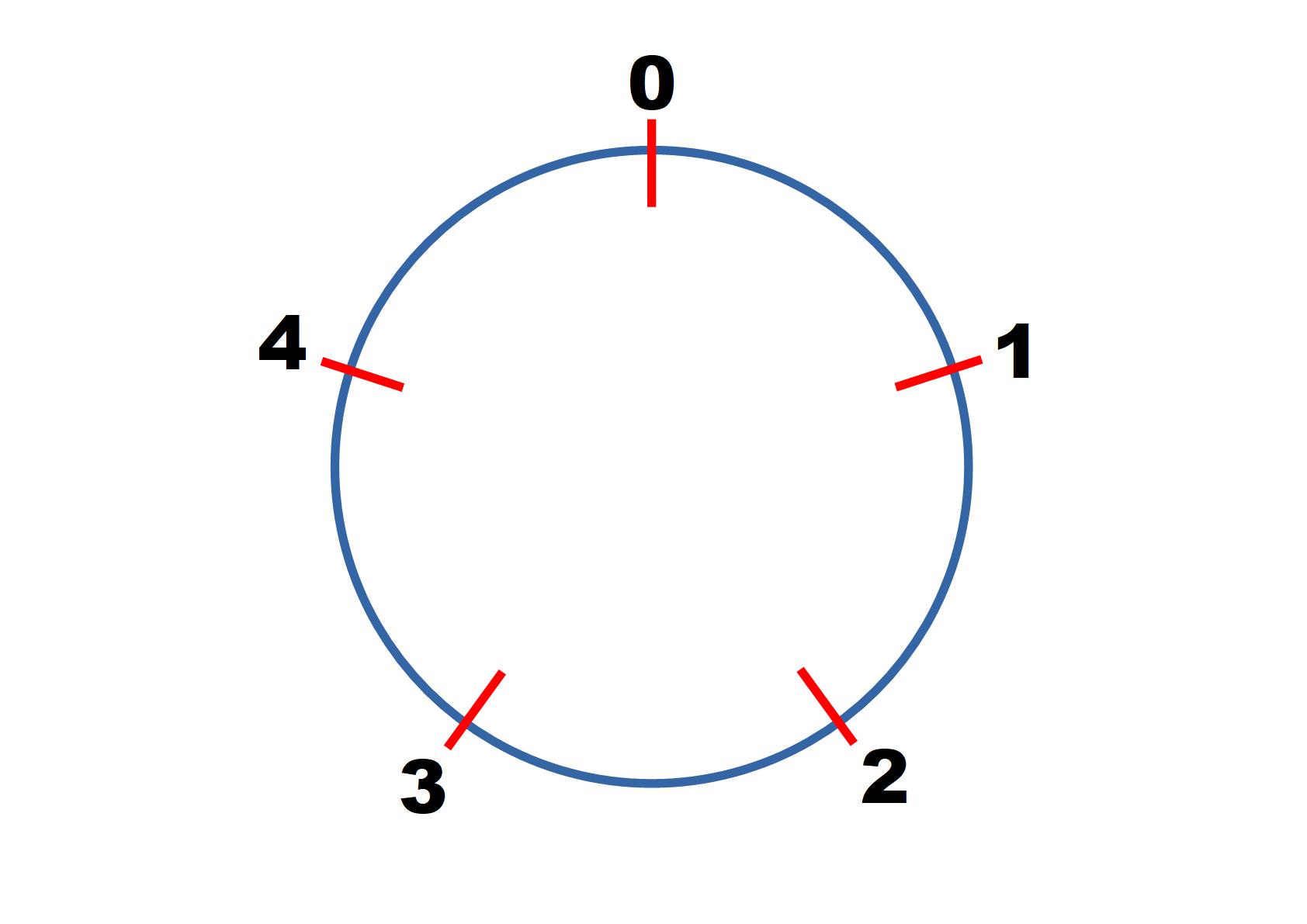
$1^2 = 1 \equiv 1 \text{ mod } 5$
$2^2 = 4 \equiv 4 \text{ mod } 5$
$3^2 = 9 \equiv 4 \text{ mod } 5$
$4^2 = ...$
$5^2 = ...$

Continue finding the value of other square numbers in modulo 5 until you notice a pattern and can predict correctly what will come next.
Can you predict the values of $100^2, 101^2, 102^2...\text{ in mod } 5$?
 

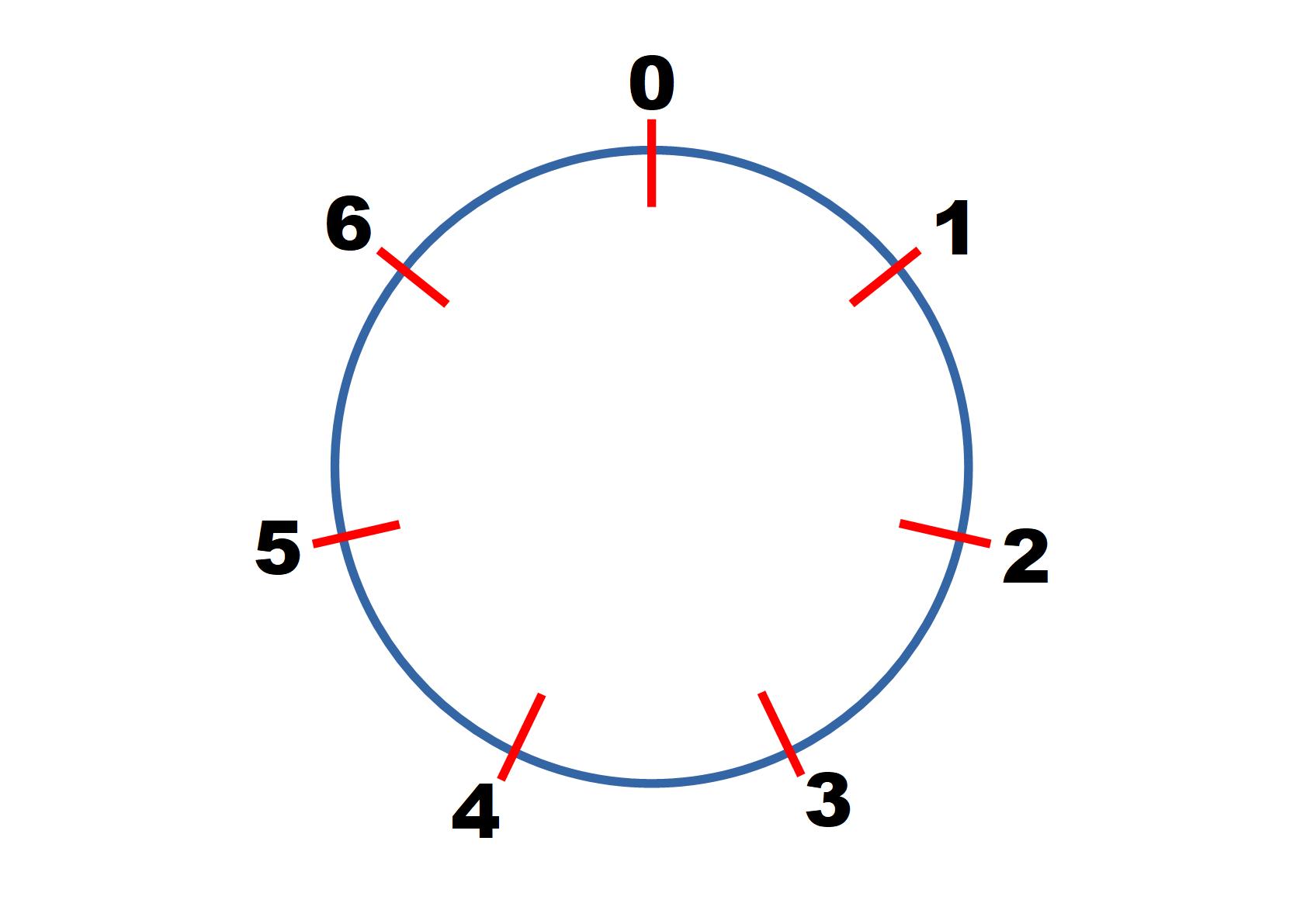
In modulo $7$ we have:

$1^2 = 1 \equiv 1 \text{ mod } 7$
$2^2 = 4 \equiv 4 \text{ mod } 7$
$3^2 = 9 \equiv 2 \text{ mod } 7$
$4^2 = 16 \equiv 2 \text{ mod } 7$

Continue finding the value of other square numbers in modulo 7 until you can predict correctly what will come next.
Can you predict the values of $100^2, 101^2, 102^2...\text{ in mod } 7?$

Investigate the value of other square numbers in modulo $11, 13, 17$... 

You may find this power modulo calculator useful!

When working in mod $p$, where $p$ is prime, how many values do you need to find before you can predict all the rest? Explain your findings.

Can you predict any values from the very start?

So far you have looked at square numbers modulo $p$, where $p$ is a prime. 
Investigate square numbers modulo $n$, where $n$ is odd but not prime, or where $n$ is even.

If you have enjoyed working on this problem, then you may enjoy Euler's Totient Function.

We are very grateful to the Heilbronn Institute for Mathematical Research for their generous support for the development of this resource.