Close to Triangular

Here are the coordinates of nine points. It is possible to draw a triangle so that the shortest distance from each point to the triangle is at most one unit.

$(0, 0)$
$(8, 2)$
$(7, 8)$
$(170, 180)$
$(340, 360)$
$(2001, 1000)$
$(1500, 750)$
$(3000, 2000)$
$(4002, 2000)$

Can you find a suitable triangle? Is there more than one possibility?


Given three points, it is always possible to draw different triangles with edges passing through those three points - here are some examples of triangles going through the same three points:
Can you convince yourself that there are always infinitely many such triangles?


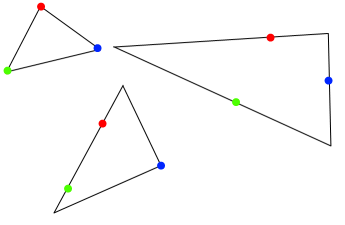
Here are some examples of different triangles going through the same set of four points:

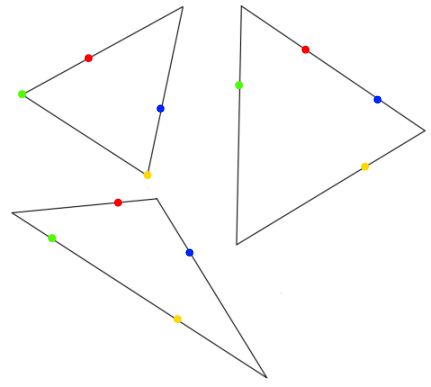
Is it always possible to draw triangles through a set of four points, whatever their position?
Investigate some examples and explain your findings.

What happens when we try to draw triangles through five points?