28 - Upward and Onward

'28 - Upward and Onward' printed from https://nrich.maths.org/

Show menu

You may like to have a go at the problem So It's 28 before trying this challenge.

We are about to explore the number 28.

In 2010 the month of February had four weeks of 7 days making 28 days altogether.

----------

Half a pack of cards with the jokers makes 28 cards altogether:

----------

The seventh triangular number is also 28:

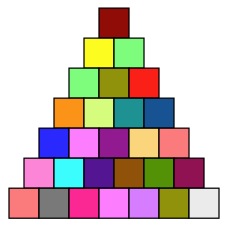
But all these examples of 28 are just flat - or you might call them 2D.

I'm suggesting we try making something 3D.

How about if we put some small cubes together and count the faces which are visible. Can we arrange the cubes so that there are exactly 28 faces?

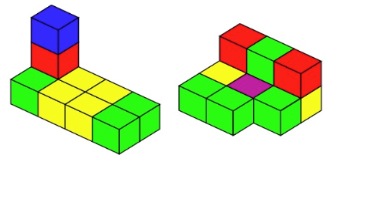
In the pictures above, we're not counting faces that are 'on the table'. I've coloured the cubes (according to how many faces are showing) to make the counting a little easier.

It would probably be good to make one of these shapes and do your own counting.

Can you arrange some cubes so that 28 of their faces are visible?

----------

You might want to try another way with a new shape resting on a glass table (you could just pretend!) so you can count the faces underneath too. Here are two shapes:

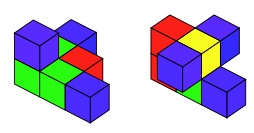
Cubes that click together might make it easier.

----------

So this is your challenge: make a shape that has 28 little square faces visible.

Now try on a pretend glass table and see how many you can make then. Any surprises?